Fill in state in CCF

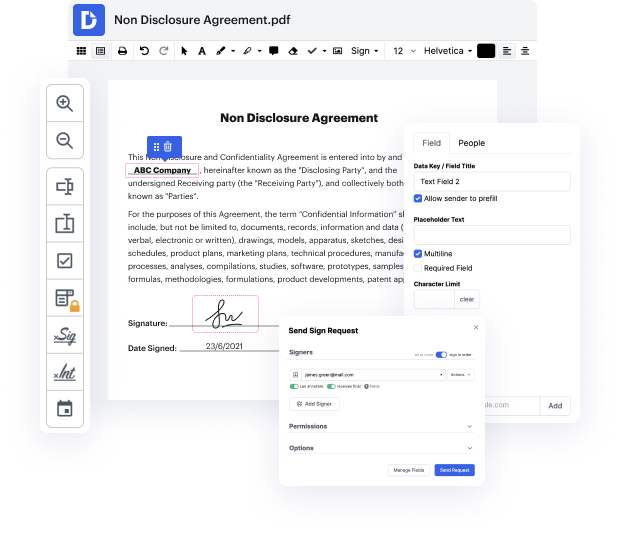
CCF may not always be the simplest with which to work. Even though many editing capabilities are available on the market, not all give a straightforward solution. We created DocHub to make editing straightforward, no matter the file format. With DocHub, you can quickly and effortlessly fill in state in CCF. On top of that, DocHub provides a range of other functionality such as document generation, automation and management, industry-compliant eSignature tools, and integrations.

DocHub also lets you save time by producing document templates from documents that you utilize frequently. On top of that, you can take advantage of our numerous integrations that allow you to connect our editor to your most utilized programs effortlessly. Such a solution makes it fast and simple to work with your files without any slowdowns.

To fill in state in CCF, follow these steps:

1. Click on Sign In or create a free account.
2. When forwarded to your Dashboard, click the Add New button and choose how you want to add your file.
3. Use our sophisticated tools that will let you improve your document's text and design.
4. Pick the ability to fill in state in CCF from the toolbar and use it on document.
5. Go over your text once more to make sure it has no mistakes or typos.
6. Click on DONE to finish editing document.

DocHub is a helpful tool for personal and corporate use. Not only does it give a comprehensive suite of tools for document creation and editing, and eSignature implementation, but it also has a range of capabilities that come in handy for developing multi-level and straightforward workflows. Anything imported to our editor is saved risk-free according to major industry standards that protect users' data.

Make DocHub your go-to option and streamline your document-driven workflows effortlessly!