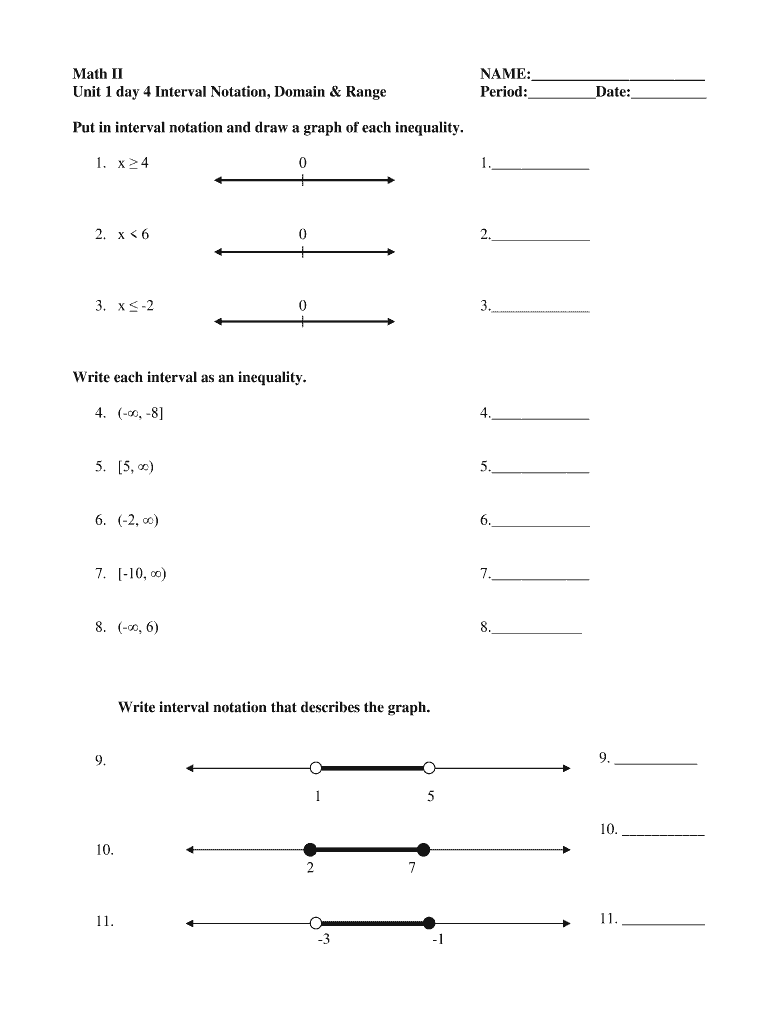
Definition and Meaning of Interval Notation Worksheet
An interval notation worksheet is an educational resource designed to help students understand and practice interval notation, a succinct way to represent a range of numbers. This format is commonly used in mathematics, particularly in algebra and calculus, to denote the domain and range of functions. Interval notation uses symbols such as parentheses and brackets to indicate whether endpoints are included in the set.
- Closed Interval [a, b]: Includes endpoints a and b.
- Open Interval (a, b): Excludes endpoints a and b.
- Mixed Interval [a, b): Includes a but excludes b.
- Special Notation: Infinity (∞) is always treated as an open endpoint, indicating that it cannot be achieved.
In addition to basic interval notation, worksheets can also incorporate exercises related to inequalities, set notation, and aspects of domain and range, providing a comprehensive learning experience.
How to Use the Interval Notation Worksheet
To effectively use an interval notation worksheet, follow these guided steps:
- Read the Instructions: Begin by reviewing the instructions provided at the top of the worksheet. This will outline the objectives and remove any ambiguities.
- Identify Intervals: Work through problems that involve identifying intervals from given inequalities or graphs. Carefully look for endpoints and their inclusion or exclusion.
- Convert Notation: Practice converting inequalities into interval notation. Focus on recognizing which symbols to use based on whether endpoints are included or excluded.
- Apply Knowledge of Domain and Range: Use the worksheet to determine the domain and range by analyzing functions or graphs. Record your findings in both interval and set notation formats.
- Check Answers: If a worksheet includes an answer key, be sure to review your work against the solutions to identify any mistakes and learn from them.
This structured approach ensures clarity and aids in the reinforcement of concepts related to interval notation.
Important Terms Related to Interval Notation Worksheet
Familiarity with the terminology associated with interval notation can greatly enhance understanding and proficiency. Key terms include:
- Interval: A set of numbers between two defined endpoints.
- Endpoint: A number that marks the end of an interval.
- Closed Interval: An interval that includes its endpoints, represented with square brackets.
- Open Interval: An interval that does not include its endpoints, represented with parentheses.
- Domain: The complete set of possible values of the independent variable for a given function.
- Range: The complete set of possible values of the dependent variable for a given function.
- Inequality: A mathematical expression that represents a relationship between values, typically using symbols like < or >.
Understanding these terms will allow learners to engage more effectively with problems on the interval notation worksheet.
Who Typically Uses the Interval Notation Worksheet
The interval notation worksheet is primarily utilized by individuals engaged in mathematics education, including:
- Middle and High School Students: Students studying algebra and pre-calculus typically use these worksheets as part of their curriculum to develop a firm grasp of intervals.
- College Students: Those enrolled in mathematics courses, particularly in calculus or analysis, also find interval notation worksheets beneficial for reinforcing their understanding of concepts.
- Educators and Tutors: Teachers and tutors employ these worksheets as supplemental materials in classroom settings or for individual instruction, helping students master this essential topic.
- Exam Preparers: Students preparing for standardized tests that include math components may practice with interval notation worksheets as part of their study routines.
This diverse usage highlights the relevance and applicability of interval notation across various educational contexts.

Examples of Using the Interval Notation Worksheet
Working through specific examples can significantly bolster comprehension of interval notation. Here are a few scenarios:
- Convert to Interval Notation: Given the inequality x > 5, the corresponding interval notation is (5, ∞).
- Interval to Inequality: For the interval [2, 6), the inequality form is 2 ≤ x < 6.
- Graph Interpretation: A graph showing a line that starts from -3 and extends infinitely in the positive direction, while including -3, would be represented as [-3, ∞).
- Domain and Range: A function f(x) that takes on values from 1 to 4, inclusive, has a range represented as [1, 4].
Using specific examples like these provides practical experience with how interval notation operates in real-world contexts.
Steps to Complete the Interval Notation Worksheet
To ensure a thorough and successful completion of an interval notation worksheet, consider these steps:
- Analyze Each Problem: Read each question carefully and identify what is asked regarding intervals or inequalities.
- Work Through Conversions: For problems requiring conversions, write down the intervals or inequalities before making the conversion to ensure clarity.
- Draw Graphs If Necessary: If instructions allow, drawing a quick graph can help visualize the intervals and make the translation to notation easier.
- Complete All Exercises: Address every exercise on the worksheet to fully engage with the material, even if it feels repetitive at times.
- Review and Correct: After completing the worksheet, go back and review your answers. Use an answer key, if available, to check your work and understand any errors.
Following this structured approach can enhance your learning experience, leading to improved mastery of interval notation concepts.