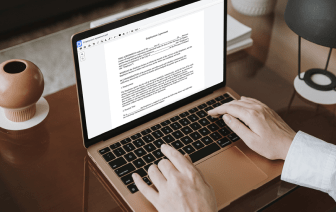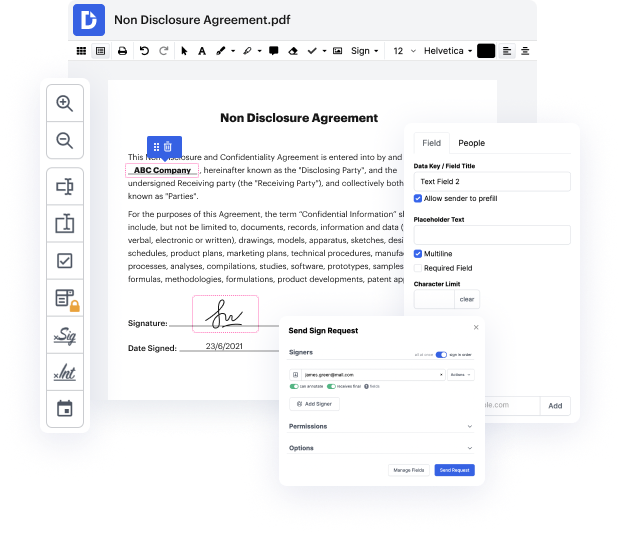
Elegir la solución ideal de gestión de archivos para su empresa puede llevar tiempo. Debe evaluar todos los matices de la aplicación que está considerando, comparar planes de precios y mantenerse al tanto de los estándares de seguridad. Sin duda, la oportunidad de manejar todos los formatos, incluido ODOC, es muy importante al considerar una plataforma. DocHub ofrece un conjunto sustancial de capacidades y herramientas para garantizar que gestione tareas de cualquier complejidad y maneje el formato de archivo ODOC. Obtenga una cuenta de DocHub, configure su espacio de trabajo y comience a trabajar con sus documentos.
DocHub es un programa integral todo en uno que le permite modificar sus documentos, firmarlos electrónicamente y crear plantillas reutilizables para los formularios más utilizados. Proporciona una interfaz de usuario intuitiva y la oportunidad de manejar sus contratos y acuerdos en formato de archivo ODOC de manera simplificada. No necesita preocuparse por estudiar numerosos tutoriales y sentirse ansioso porque la aplicación es demasiado compleja. configure capítulo en ODOC, delegue campos rellenables a los destinatarios designados y recoja firmas fácilmente. DocHub se trata de capacidades poderosas para expertos de todos los antecedentes y necesidades.
Mejore sus procedimientos de generación y aprobación de archivos con DocHub ahora mismo. Disfrute de todo esto utilizando una prueba gratuita y actualice su cuenta cuando esté listo. Edite sus documentos, cree formularios y aprenda todo lo que puede hacer con DocHub.
un conjunto es una colección de objetos que llamamos elementos que podrían significar objetos físicos, pensamientos, ideas y conceptos, incluidos objetos matemáticos, que serán, por supuesto, el enfoque principal para nosotros. Posiblemente más importante, un conjunto es una forma de empaquetar objetos que comparten propiedades similares de manera significativa. Considera el conjunto de triángulos; podemos afirmar sin ambigüedad si algo está o no en este conjunto. Esto está, así que esto, pero esta forma no está; no es un triángulo. Esta falta de ambigüedad en lo que es o no es un conjunto es fundamental para la teoría de conjuntos. También podemos hacer afirmaciones sobre el conjunto y evaluar nuevamente sin ambigüedad si son verdaderas o falsas. Es cierto que un elemento del conjunto de triángulos tiene tres lados, pero no es cierto que la suma de los ángulos internos sea 360 grados. Un conjunto que contiene los números 1, 2 y 3 se escribiría así, con llaves y los elementos separados por comas. Podemos nombrar el conjunto; en este caso, si decimos que a es igual al conjunto 1, 2 y 3, podemos jus