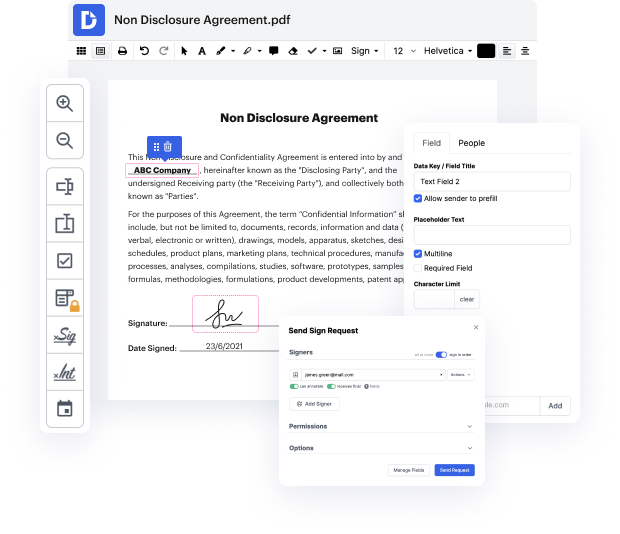
Si deseas aplicar un pequeño ajuste al documento, no debería tomar mucho tiempo Notificación de fórmula de gráfico. Este tipo de acción simple no tiene que requerir capacitación adicional ni pasar por manuales para aprenderlo. Usando la herramienta de modificación de documentos adecuada, no tomarás más tiempo del necesario para un cambio tan rápido. Usa DocHub para simplificar tu proceso de modificación, independientemente de si eres un usuario experimentado o si es la primera vez que utilizas un servicio de editor en línea. Este instrumento requerirá unos minutos para averiguar cómo Notificación de fórmula de gráfico. Lo único que se necesita para ser más productivo con la edición es una cuenta de DocHub.
Un editor de documentos simple como DocHub te ayudará a optimizar la cantidad de tiempo que necesitas dedicar a la modificación de documentos, independientemente de tu conocimiento previo de este tipo de instrumentos. ¡Crea una cuenta ahora y aumenta tu eficiencia de inmediato con DocHub!
este es un reticulado, es un conjunto de puntos espaciados uniformemente en una cuadrícula repetitiva. los puntos de reticulado aquí se representan como estando en las intersecciones de las líneas punteadas. este es un polígono de reticulado simple, es un polígono tal que cada una de sus esquinas se encuentra en los puntos de reticulado y se llama simple porque sus líneas no se superponen ni cruzan y no contiene agujeros. indicamos el número de puntos de reticulado en el límite del polígono como B y el número de puntos de reticulado interiores que se encuentran estrictamente dentro del límite del polígono como I. dado un polígono de reticulado simple y se nos pide encontrar esta área, es fácil perderse en la trigonometría complicada cuando en realidad hay una fórmula simple conocida como teorema de Pix, que se aplica a cualquier polígono de reticulado simple. el teorema de Pix, descrito por Geogpick en 1899, dice que el área de un polígono de reticulado simple A es igual al número de puntos de reticulado interiores más la mitad del número de puntos de reticulado en el límite menos uno. en este video, demostraremos este teorema fi
