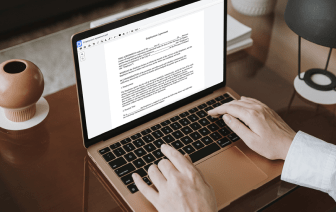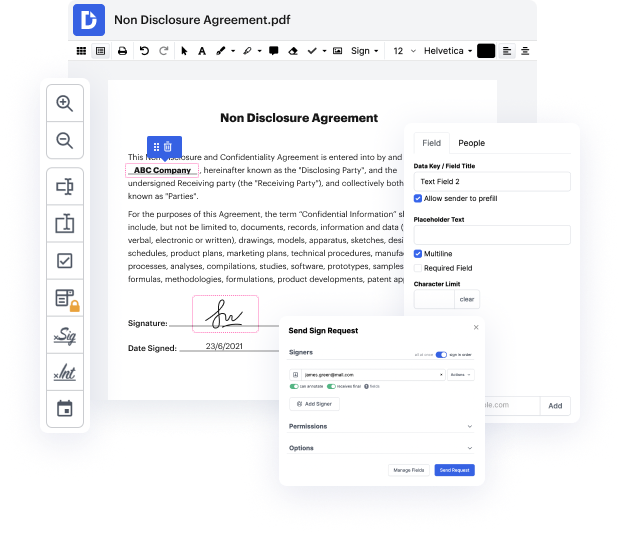
Los formatos de archivo inusuales en su gestión y edición de documentos diaria pueden crear confusión instantánea sobre cómo modificarlos. Puede que necesite más que el software de computadora preinstalado para una edición de archivos efectiva y rápida. Si necesita vincular un círculo en CWK o hacer cualquier otro cambio simple en su archivo, elija un editor de documentos que tenga las características para que pueda manejarlo con facilidad. Para lidiar con todos los formatos, como CWK, optar por un editor que funcione correctamente con todo tipo de documentos será su mejor opción.
Pruebe DocHub para una gestión de archivos efectiva, independientemente del formato de su documento. Tiene potentes herramientas de edición en línea que agilizan sus operaciones de gestión de documentos. Puede crear, editar, anotar y compartir cualquier archivo fácilmente, ya que todo lo que necesita para acceder a estas características es una conexión a internet y un perfil activo de DocHub. Solo una herramienta de documentos es todo lo que necesita. No pierda tiempo cambiando entre varias aplicaciones para diferentes documentos.
Disfrute de la eficiencia de trabajar con una herramienta hecha específicamente para agilizar el procesamiento de documentos. Vea lo fácil que es revisar cualquier archivo, incluso cuando es la primera vez que ha trabajado con su formato. Regístrese para obtener una cuenta gratuita ahora y mejore todo su proceso de trabajo.
hola en este video voy a mirar un problema particular de programación de computadoras es un problema de programación de gráficos por computadora voy a mirarlo usando p5.js y JavaScript pero las ideas se traducirían a muchos entornos diferentes y cuál es ese problema así que cuando vengan aquí a diagramarlo para ustedes digamos que tienes un lienzo en el que estás dibujando y tu objetivo es que quieres llenar este lienzo con círculos y pongo los círculos todos aleatoriamente en el lienzo así que el objetivo es que el lienzo se vea finalmente algo así ahora nota la forma en que dibujé esto ninguno de estos círculos se superpone la verdad es que si solo intentas dibujar cien círculos en un lienzo en una ventana lo más probable es que a través de la probabilidad aleatoria y el azar se superpongan así que ¿cómo garantizas que no se superpongan? ahora probablemente hay una variedad de soluciones para esto una de las cuales acabo de pensar que creo que sería genial demostrar