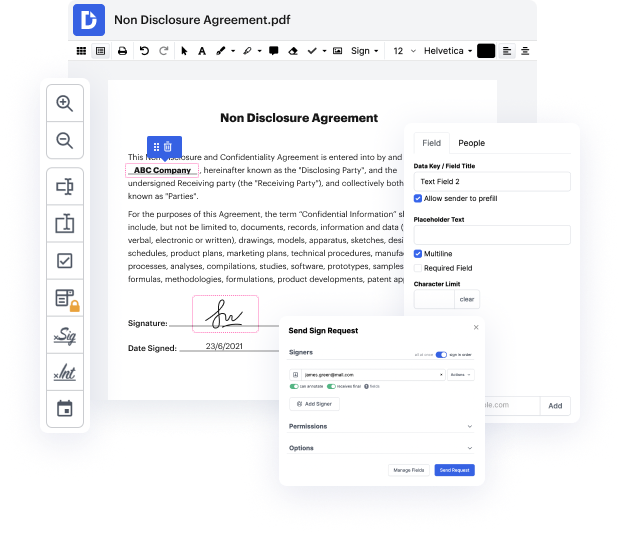
Ya sea que estés acostumbrado a trabajar con RPT o gestionando este formato por primera vez, editarlo no debería sentirse como un desafío. Diferentes formatos pueden requerir aplicaciones específicas para abrirlos y editarlos correctamente. Sin embargo, si necesitas corregir rápidamente un punto en RPT como parte de tu proceso habitual, lo mejor es conseguir una herramienta multifuncional de documentos que permita todo tipo de operaciones sin esfuerzo adicional.
Prueba DocHub para una edición simplificada de RPT y otros formatos de documentos. Nuestra plataforma proporciona un procesamiento de documentos sin esfuerzo, sin importar cuánta o poca experiencia previa tengas. Con herramientas que te permiten trabajar en cualquier formato, no necesitarás cambiar entre ventanas de edición al trabajar con cada uno de tus documentos. Crea, edita, anota y comparte tus documentos fácilmente para ahorrar tiempo en tareas menores de edición. Solo necesitarás registrarte para obtener una nueva cuenta de DocHub, y luego podrás comenzar tu trabajo de inmediato.
Observa una mejora en la productividad del procesamiento de documentos con el conjunto de características simples de DocHub. Edita cualquier documento rápida y fácilmente, independientemente de su formato. Disfruta de todas las ventajas que provienen de la eficiencia y conveniencia de nuestra plataforma.
gracias por ver y hoy quiero usar el teorema del valor intermedio para mostrar que la función tiene un punto fijo más precisamente supongamos que tienes una función f de 0 a 1 a 0 a 1 así que esto solo significa que F está entre 0 y 1 y somos continuos entonces f tiene un punto fijo como un punto fijo ¿qué significa eso? significa que hay un punto específico piensa en 1/2 de modo que si aplicas F a él entonces no pasa nada así que hay un X naught en algún lugar del intervalo 0 coma 1 tal que f de X naught es igual a X naught en otras palabras este punto es fijo por F así que no pasa nada aquí y de hecho hay una bonita interpretación geométrica de esto porque todo lo que esto significa es que si tienes una función así de 0 a 1 a 0 a 1 por ejemplo así supongamos que F se ve así que F debe cruzar la línea y igual a x más o menos así en otras palabras debe haber algún punto X naught tal que la salida de X naught es la misma cosa y te daré algunas aplicaciones interesantes en un segundo pero primero