Hay numerosas herramientas de edición de documentos en el mercado, pero solo unas pocas son adecuadas para todos los formatos de archivo. Algunas herramientas son, por el contrario, versátiles pero difíciles de usar. DocHub proporciona la solución a estos desafíos con su editor basado en la nube. Ofrece ricas capacidades que te permiten realizar tus tareas de gestión de documentos de manera eficiente. Si necesitas identificar Faint rápidamente en 1ST, ¡DocHub es la opción ideal para ti!
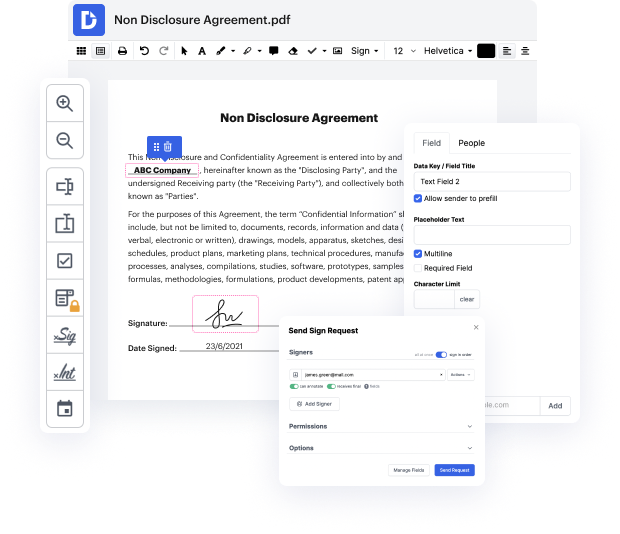
Nuestro proceso es extremadamente fácil: importas tu archivo 1ST a nuestro editor → se transforma automáticamente en un formato editable → aplicas todos los ajustes esenciales y lo actualizas profesionalmente. Solo necesitas un par de momentos para completar tu trabajo.
Después de aplicar todos los cambios, puedes convertir tu documentación en una plantilla multiusos. Solo necesitas ir al Menú del lado izquierdo de nuestro editor y hacer clic en Acciones → Convertir a Plantilla. Encontrarás tu documentación almacenada en una carpeta separada en tu Tablero, ahorrándote tiempo la próxima vez que necesites el mismo formulario. ¡Prueba DocHub hoy!
Los instrumentos débiles se refieren a un escenario donde los variables instrumentales están solo débilmente correlacionados con las variables explicativas endógenas. ¿Por qué sería eso un problema? Entonces, el caso de los instrumentos débiles aquí se refiere a esta correlación entre X y Z. Si X y Z no están fuertemente correlacionados, entonces la estimación del variable instrumental puede ser muy imprecisa y puede estar sesgada. Para entender por qué ese es el caso, veamos la ecuación para calcular la estimación del variable instrumental para beta aquí. Así que esas son las ecuaciones. Podemos ver que beta es esta correlación entre Z y Y dividida por la correlación X y Z y ¿por qué es eso? Bueno, si consideras cuál es la correlación implícita del modelo entre Z y Y, es la correlación Z X multiplicada por este coeficiente de regresión beta aquí y a partir de ahí puedes resolver para beta. Entonces, ¿por qué sería un problema si esta correlación es muy pequeña? Es un problema porque entonces la variación de muestreo de esa correlación - lo que sea