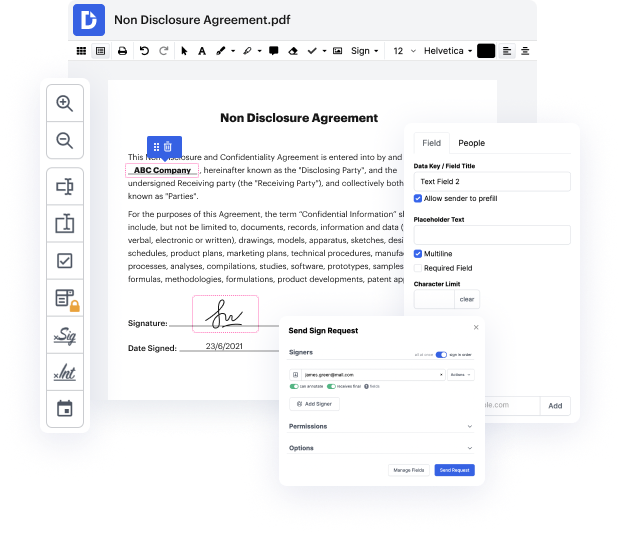
Trabajar con documentos como el registro puede parecer un desafío, especialmente si es la primera vez que trabajas con este tipo. A veces, incluso una pequeña edición puede causar un gran dolor de cabeza cuando no sabes cómo trabajar con el formato y evitar hacer un caos del proceso. Cuando se te asigna cortar un punto en el registro, siempre puedes hacer uso de un software de edición de imágenes. Otros pueden optar por un editor de texto clásico, pero se quedan atascados cuando se les pide reformatear. Con DocHub, sin embargo, manejar un registro no es más difícil que editar un documento en cualquier otro formato.
Prueba DocHub para una edición rápida y productiva de documentos, independientemente del formato del documento que tengas en tus manos o del tipo de documento que necesites corregir. Esta solución de software es en línea, accesible desde cualquier navegador con acceso a internet estable. Modifica tu registro justo cuando lo abres. Hemos desarrollado la interfaz para asegurar que incluso los usuarios sin experiencia previa puedan hacer todo lo que necesitan. Optimiza la edición de tus documentos con una solución elegante para cualquier tipo de documento.
Trabajar con diferentes tipos de documentos no debería sentirse como ciencia espacial. Para optimizar tu tiempo de edición de documentos, necesitas una plataforma rápida como DocHub. Gestiona más con todas nuestras herramientas al alcance de tu mano.
saludo a los estudiantes y bienvenidos de nuevo a otra lección sobre variables complejas en este video voy a definir puntos de ramificación y cortes de ramificación y construir una base que nos permitirá realizar integración compleja de funciones con ramificaciones para construir esta base comenzaré discutiendo el logaritmo natural de un número complejo Z supongamos que tengo una función W igual a F de Z que es igual a lon de Z si recuerdas mi primer video sobre variables complejas recordarás que puedo escribir cualquier número complejo como su parte real más I veces su parte imaginaria en el caso de W puedo escribirlo como u más IV donde u y v son números reales también puedo escribir un número complejo Z en el plano complejo como una representación polar con Z siendo la distancia desde el origen R veces la exponencial de I veces el ángulo relativo al eje real positivo theta en ese caso el logaritmo natural de Z se convertirá en el logaritmo natural de R más I veces theta nota que R y theta son ambos números reales positivos si ahora reorganizo esta ecuación