Not all formats, including binary, are created to be effortlessly edited. Even though many tools can help us edit all form formats, no one has yet created an actual all-size-fits-all tool.
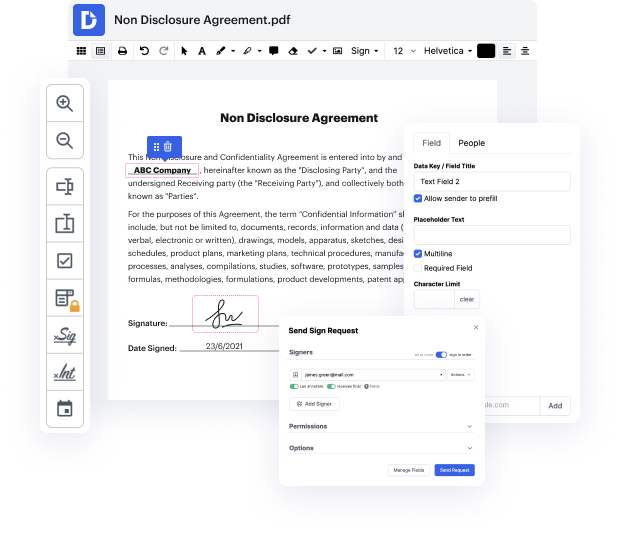
DocHub gives a straightforward and streamlined tool for editing, managing, and storing documents in the most widely used formats. You don't have to be a technology-savvy person to wipe highlight in binary or make other changes. DocHub is powerful enough to make the process straightforward for everyone.
Our feature enables you to modify and edit documents, send data back and forth, create interactive forms for data collection, encrypt and protect paperwork, and set up eSignature workflows. Moreover, you can also create templates from documents you utilize on a regular basis.
You’ll find plenty of other functionality inside DocHub, including integrations that let you link your binary form to a variety productivity applications.
DocHub is a simple, fairly priced way to manage documents and streamline workflows. It offers a wide range of features, from creation to editing, eSignature services, and web document developing. The application can export your paperwork in many formats while maintaining greatest security and adhering to the highest data security standards.
Give DocHub a go and see just how straightforward your editing operation can be.
hi Iamp;#39;m Joe James and this video is going to cover binary search trees so a tree is a collection of nodes with edges that connect them the nodes are organized into levels and the top level is called the root node each node can have child nodes in this case the three is a parent node and it has a left child and a right child and the left and right child are called siblings because they share the same parents the 1 4 6 and nine nodes here are called Leaf nodes because they donamp;#39;t have any child nodes in a binary tree each node can have up to two child nodes a left child and a right child node fiveamp;#39;s right sub tree includes everything in this triangle which is a tree in itself under node five node 5amp;#39;s left sub tree includes noes 3 1 and four node four has ancestors which are simply every node between itself and the root node and node five has descendants but basically every node below it all of this children node and their childrenamp;#39;s nodes and so on i