Wipe heading in binary

Utilize this walkthrough to wipe heading in binary quickly

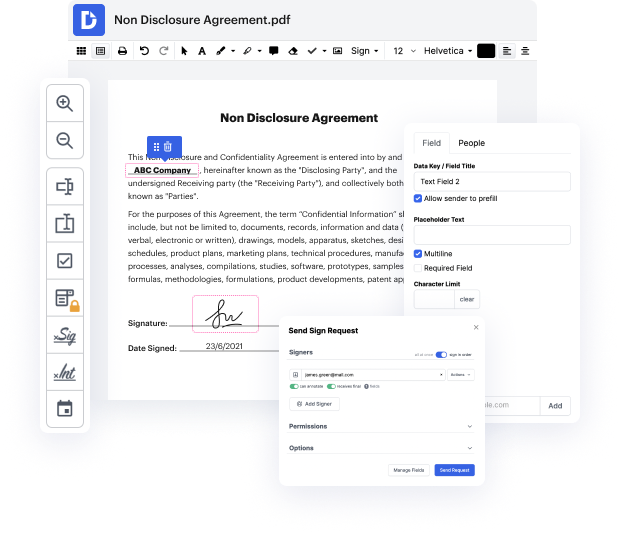
binary may not always be the simplest with which to work. Even though many editing capabilities are available on the market, not all offer a straightforward tool. We created DocHub to make editing easy, no matter the document format. With DocHub, you can quickly and easily wipe heading in binary. Additionally, DocHub delivers a range of other features including form generation, automation and management, sector-compliant eSignature tools, and integrations.

DocHub also allows you to save time by creating form templates from paperwork that you use regularly. Additionally, you can benefit from our a wide range of integrations that allow you to connect our editor to your most utilized applications effortlessly. Such a tool makes it fast and simple to deal with your files without any delays.

To wipe heading in binary, follow these steps:

Hit Sign In or register a free account.
When directed to your Dashboard, hit the Add New button and choose how you want to add your document.
Use our pro tools that can help you enhance your document's text and layout.
Pick the option to wipe heading in binary from the toolbar and use it on form.
Check your text once more to make sure it has no mistakes or typos.
Hit DONE to complete editing form.

DocHub is a helpful feature for individual and corporate use. Not only does it offer a all-purpose set of tools for form generation and editing, and eSignature implementation, but it also has a range of capabilities that come in handy for developing complex and straightforward workflows. Anything imported to our editor is stored safe in accordance with leading field requirements that protect users' information.

Make DocHub your go-to option and simplify your form-driven workflows effortlessly!

PDF editing simplified with DocHub

Seamless PDF editing

Editing a PDF is as simple as working in a Word document. You can add text, drawings, highlights, and redact or annotate your document without affecting its quality. No rasterized text or removed fields. Use an online PDF editor to get your perfect document in minutes.

Smooth teamwork

Collaborate on documents with your team using a desktop or mobile device. Let others view, edit, comment on, and sign your documents online. You can also make your form public and share its URL anywhere.

Automatic saving

Every change you make in a document is automatically saved to the cloud and synchronized across all devices in real-time. No need to send new versions of a document or worry about losing information.

Google integrations

DocHub integrates with Google Workspace so you can import, edit, and sign your documents directly from your Gmail, Google Drive, and Dropbox. When finished, export documents to Google Drive or import your Google Address Book and share the document with your contacts.

Powerful PDF tools on your mobile device

Keep your work flowing even when you're away from your computer. DocHub works on mobile just as easily as it does on desktop. Edit, annotate, and sign documents from the convenience of your smartphone or tablet. No need to install the app.

Secure document sharing and storage

Instantly share, email, and fax documents in a secure and compliant way. Set a password, place your documents in encrypted folders, and enable recipient authentication to control who accesses your documents. When completed, keep your documents secure in the cloud.

Drive efficiency with the DocHub add-on for Google Workspace

Access documents and edit, sign, and share them straight from your favorite Google Apps.

Install now

How to wipe heading in binary

4.8 out of 5

72 votes

hi Iamp;#39;m Joe James and this video is going to cover binary search trees so a tree is a collection of nodes with edges that connect them the nodes are organized into levels and the top level is called the root node each node can have child nodes in this case the three is a parent node and it has a left child and a right child and the left and right child are called siblings because they share the same parents the 1 4 6 and nine nodes here are called Leaf nodes because they donamp;#39;t have any child nodes in a binary tree each node can have up to two child nodes a left child and a right child node fiveamp;#39;s right sub tree includes everything in this triangle which is a tree in itself under node five node 5amp;#39;s left sub tree includes noes 3 1 and four node four has ancestors which are simply every node between itself and the root node and node five has descendants but basically every node below it all of this children node and their childrenamp;#39;s nodes and so on i

Got questions?

Below are some common questions from our customers that may provide you with the answer you're looking for. If you can't find an answer to your question, please don't hesitate to reach out to us.

Contact us

What is the binary for the space character?

Character NameCharBinary Space 00100000 Exclamation Point ! 00100001 Double Quote 00100010 Pound/Number Sign # 0010001179 more rows

What is the binary code for AZ?

The binary equivalent of a character is the binary representation of its ASCII code. The binary equivalents of characters A-Z in upper and lower cases are: Upper case A-Z: 01000001 - 01011010. Lower case a-z: 01100001 - 01111010.

What is new line in binary?

When reading in text mode, the native newline sequence is translated back to \n. In binary mode, no translation is performed, and the internal representation produced by \n is output directly.

How to remove leading zeros in binary?

Heres one way to do it: # Remove n leading zeroes from binary number. def removeleadingzeroes(binarynumber, n): binarynumber = binarynumber[n:] return binarynumber. # Add n leading zeroes to binary number. def addleadingzeroes(binarynumber, n): binarynumber = 0*n + binarynumber. return binarynumber.

How do we represent text in binary?

The ASCII code takes each character on the keyboard and assigns it a binary number. For example: the letter a has the binary number 0110 0001 (this is the denary number 97) the letter b has the binary number 0110 0010 (this is the denary number 98)

How do you break binary code?

Remember that in binary 1 is on: and 0 is off. Choose the binary number that you want to decode. Give each number a value, starting from the extreme right. For example, using the number 1001001, 1=1, +0=2, +0=4, +1=8, +0=16, +0=32, +1=64.

What is 00001010 in binary?

Table of Binary, Hexadecimal and ASCII values, BinaryDecimalHexadecimal 00001010 10 A 00001011 11 B 00001100 12 C 00001101 13 D124 more rows

What is the LF in binary?

LF ( 0 0 0 1010 ) represented a line feed, moving the printing head down one line.

See why our customers choose DocHub

Great solution for PDF docs with very little pre-knowledge required.

"Simplicity, familiarity with the menu and user-friendly. It's easy to navigate, make changes and edit whatever you may need. Because it's used alongside Google, the document is always saved, so you don't have to worry about it."

Pam Driscoll F
Teacher

A Valuable Document Signer for Small Businesses.

"I love that DocHub is incredibly affordable and customizable. It truly does everything I need it to do, without a large price tag like some of its more well known competitors. I am able to send secure documents directly to me clients emails and via in real time when they are viewing and making alterations to a document."

Jiovany A
Small-Business

I can create refillable copies for the templates that I select and then I can publish those.

"I like to work and organize my work in the appropriate way to meet and even exceed the demands that are made daily in the office, so I enjoy working with PDF files, I think they are more professional and versatile, they allow..."

Victoria G
Small-Business

be ready to get more

Edit and sign PDFfor free

Get started now