Vary sample in 1ST

Use this quick tutorial to vary sample in 1ST with swift ease

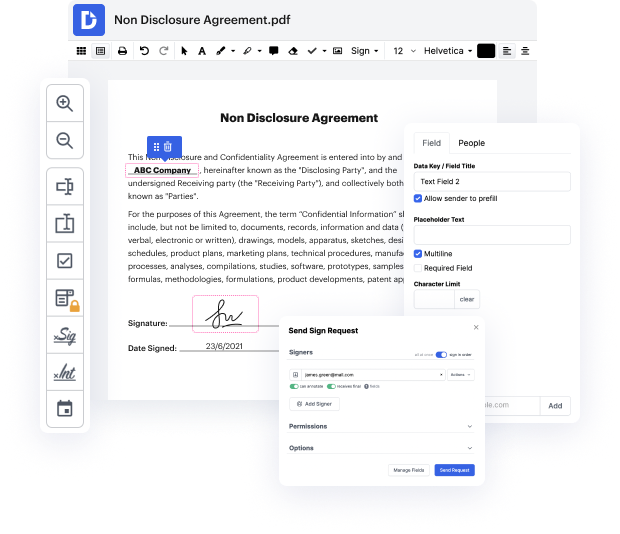
Disadvantages exist in every solution for editing every file type, and although you can use a lot of solutions on the market, not all of them will suit your specific requirements. DocHub makes it easier than ever to make and change, and manage papers - and not just in PDF format.

Every time you need to swiftly vary sample in 1ST, DocHub has got you covered. You can effortlessly modify document components including text and pictures, and layout. Personalize, arrange, and encrypt files, build eSignature workflows, make fillable documents for intuitive data gathering, etc. Our templates feature allows you to generate templates based on papers with which you frequently work.

In addition, you can stay connected to your go-to productivity tools and CRM platforms while handling your files.

vary sample in 1ST by following these steps:

Set up your DocHub account or sign in if you already have one.
Click the Add New button to upload or import your 1ST into the editor. Additionally, you can use the tools available to tweak the text and personalize the layout.
Select the option to vary sample in 1ST from the menu bar and apply it to the document.
Go through your document again to ensure that you haven’t overlooked any errors or typos. When you complete, click DONE.
You can then share your file with others or send it out utilizing your selected way.

One of the most remarkable things about leveraging DocHub is the ability to handle document tasks of any difficulty, regardless of whether you need a quick modify or more diligent editing. It comes with an all-in-one document editor, website form builder, and workflow-centered tools. In addition, you can be sure that your papers will be legally binding and comply with all security protocols.

Cut some time off your projects with the help of DocHub's features that make managing files effortless.

PDF editing simplified with DocHub

Seamless PDF editing

Editing a PDF is as simple as working in a Word document. You can add text, drawings, highlights, and redact or annotate your document without affecting its quality. No rasterized text or removed fields. Use an online PDF editor to get your perfect document in minutes.

Smooth teamwork

Collaborate on documents with your team using a desktop or mobile device. Let others view, edit, comment on, and sign your documents online. You can also make your form public and share its URL anywhere.

Automatic saving

Every change you make in a document is automatically saved to the cloud and synchronized across all devices in real-time. No need to send new versions of a document or worry about losing information.

Google integrations

DocHub integrates with Google Workspace so you can import, edit, and sign your documents directly from your Gmail, Google Drive, and Dropbox. When finished, export documents to Google Drive or import your Google Address Book and share the document with your contacts.

Powerful PDF tools on your mobile device

Keep your work flowing even when you're away from your computer. DocHub works on mobile just as easily as it does on desktop. Edit, annotate, and sign documents from the convenience of your smartphone or tablet. No need to install the app.

Secure document sharing and storage

Instantly share, email, and fax documents in a secure and compliant way. Set a password, place your documents in encrypted folders, and enable recipient authentication to control who accesses your documents. When completed, keep your documents secure in the cloud.

Drive efficiency with the DocHub add-on for Google Workspace

Access documents and edit, sign, and share them straight from your favorite Google Apps.

Install now

How to vary sample in 1ST

4.6 out of 5

50 votes

Estimates, like the sample mean or sample standard deviation, can change with each new sample. Understanding this fluctuation is central to developing a foundation for understanding the quality of parameter estimates. This video accompanies the discussion of *Variability in Estimates* in OpenIntro Statistics. Here, we will learn about point estimates, and see that point estimates are not exact. We will also have our first opportunity to quantify variability in estimates by studying the standard error of the mean. Finally, we will conclude with a summary of a few basic properties of point estimates. Suppose we want to estimate the population mean based on a sample. The most intuitive way to go about doing this is to simply take the sample mean. The sample mean is called a point estimate of the population mean: if we can only choose one value to estimate the population mean, this is our best guess. If we take a new sample and recompute the mean, we will probably not get the exact same an

Related features

Shade chart in the Registration Rights Agreement

Shade chart in the Assumption Agreement

Shade chart in the Contribution Agreement

Shade chart in the Deposit Agreement

Shade chart in the Marketing Agreement

Shade chart in the Merger Agreement

Shade chart in the Proprietary Information Agreement

Shade chart in the Concession Agreement

Got questions?

Below are some common questions from our customers that may provide you with the answer you're looking for. If you can't find an answer to your question, please don't hesitate to reach out to us.

Contact us

How do the sample vary?

Every sample is different as we are selecting only a few units from the entire population for the purpose of some study. So the statistics (mean, median, mode, s.d. etc) from one sample will differ from that of other sample.

Why is the sample variance n 1?

The reason dividing by n-1 corrects the bias is because we are using the sample mean, instead of the population mean, to calculate the variance. Since the sample mean is based on the data, it will get drawn toward the center of mass for the data.

How do you use vary in a sentence?

Examples of vary in a Sentence The cost of a room at the hotel varies with the season. Their services vary depending on the customer. Theyve tried to improve their procedures, with varying degrees of success.

What does n-1 mean in statistics?

The purpose of using n-1 is so that our estimate is unbiased in the long run. What this means is that if we take a second sample, well get a different value of s. If we take a third sample, well get a third value of s, and so on. We use n-1 so that the average of all these values of s is equal to . Review and intuition why we divide by n-1 for the unbiased Khan Academy more-standard-deviation Khan Academy more-standard-deviation

What does it mean to vary something?

verb transitiveWord forms: ˈvaried or ˈvarying. 1. to change in form, appearance, nature, substance, etc.; alter; modify. 2. to make different from one another.

Why is there n-1 in sample variance on Reddit?

Division by N is slightly biased (it is an underestimate on average), so its common to divide by N-1 because it gives an unbiased estimator (if you care about unbiasedness). Division by N actually gives an estimator with slighly lower mean squared error. Why do we divide by n - 1 when calculating sample variance? - Reddit Reddit statistics comments whydo Reddit statistics comments whydo

Why do we do n-1 in sample variance?

Now, when you calculate the variance for a population, you divide by the number of data points, or n. But when youre working with a sample, you divide by n - 1. Why? The simple reason is this: using n - 1 instead of n gives a more accurate idea of how spread out the actual population is, based on your sample. Why Sample Variance Uses n - 1: A Simple Explanation with LinkedIn pulse why-sample-variance LinkedIn pulse why-sample-variance

Why use n-1 instead of n in standard deviation?

The n-1 equation is used in the common situation where you are analyzing a sample of data and wish to make more general conclusions. The SD computed this way (with n-1 in the denominator) is your best guess for the value of the SD in the overall population. Why use n-1 when calculating a standard deviation? - FAQ 1383 GraphPad support faqid GraphPad support faqid

See why our customers choose DocHub

Great solution for PDF docs with very little pre-knowledge required.

"Simplicity, familiarity with the menu and user-friendly. It's easy to navigate, make changes and edit whatever you may need. Because it's used alongside Google, the document is always saved, so you don't have to worry about it."

Pam Driscoll F
Teacher

A Valuable Document Signer for Small Businesses.

"I love that DocHub is incredibly affordable and customizable. It truly does everything I need it to do, without a large price tag like some of its more well known competitors. I am able to send secure documents directly to me clients emails and via in real time when they are viewing and making alterations to a document."

Jiovany A
Small-Business

I can create refillable copies for the templates that I select and then I can publish those.

"I like to work and organize my work in the appropriate way to meet and even exceed the demands that are made daily in the office, so I enjoy working with PDF files, I think they are more professional and versatile, they allow..."

Victoria G
Small-Business

be ready to get more

Edit and sign PDFfor free

Get started now