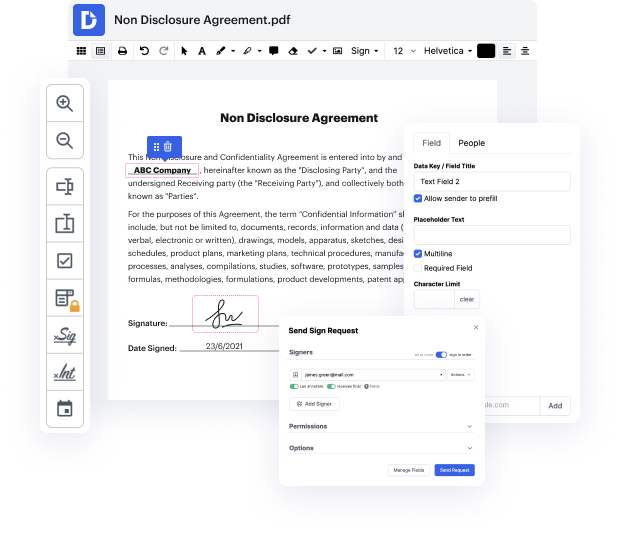
No matter how complex and difficult to edit your files are, DocHub provides an easy way to modify them. You can change any part in your AFP with no effort. Whether you need to fine-tune a single element or the whole form, you can rely on our powerful tool for fast and quality results.
In addition, it makes certain that the final document is always ready to use so that you’ll be able to get on with your tasks without any slowdowns. Our extensive group of capabilities also includes pro productivity tools and a library of templates, enabling you to take full advantage of your workflows without losing time on recurring operations. Moreover, you can gain access to your documents from any device and integrate DocHub with other solutions.
DocHub can handle any of your form management operations. With an abundance of capabilities, you can generate and export paperwork however you choose. Everything you export to DocHub’s editor will be stored safely for as long as you need, with strict security and information security frameworks in place.
Check DocHub now and make managing your files easier!
So today weamp;#39;re going to be taking our first step with monads which is the main topic of the first half of the course but as usual weamp;#39;re going to kick things off with a quick review of what weamp;#39;ve done so far so what we started off with a couple of lectures ago is the idea of generalizing our old friend the map operation from lists to other data structures and this gave rise to the idea of whatamp;#39;s called a funter so letamp;#39;s just quickly refresh um how this actually is implemented in hascal so we have a new class declaration and itamp;#39;s saying that the class of functors takes a parameterized type called f so thatamp;#39;s something like list or tree or maybe or so on and in order to be a member of the funter class you simply just have to have an appropriate mapping operation which is a generalization of the mapping operation for lists and the mapping operation is called fmap and it takes a function from A to B so a function of one parameter and i