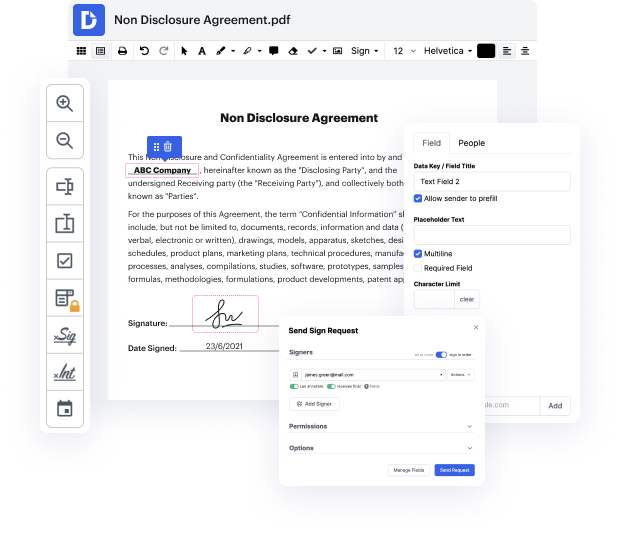
Browsing for a professional tool that handles particular formats can be time-consuming. Regardless of the huge number of online editors available, not all of them are suitable for EGT format, and certainly not all allow you to make changes to your files. To make things worse, not all of them provide the security you need to protect your devices and documentation. DocHub is a great answer to these challenges.
DocHub is a well-known online solution that covers all of your document editing needs and safeguards your work with enterprise-level data protection. It works with various formats, such as EGT, and allows you to modify such paperwork quickly and easily with a rich and user-friendly interface. Our tool fulfills crucial security certifications, like GDPR, CCPA, PCI DSS, and Google Security Assessment, and keeps improving its compliance to provide the best user experience. With everything it provides, DocHub is the most reliable way to Snip attribute in EGT file and manage all of your personal and business documentation, regardless of how sensitive it is.
As soon as you complete all of your modifications, you can set a password on your updated EGT to ensure that only authorized recipients can open it. You can also save your document with a detailed Audit Trail to check who made what edits and at what time. Opt for DocHub for any documentation that you need to edit safely. Sign up now!
PROFESSOR: Since our shortest paths tree algorithms like Dijkstras are not going to work for minimum spanning trees, we need something else. So what Im going to use is something called the cut property. Its a really beautiful, simple idea that is a little surprising that it works, as well see in a moment. But it will allow us to compute minimum spanning trees in a bunch of different ways all resting on the foundation that is known as the cut property. So the basic idea here, Im going to first introduce a term which is a cut, which is an assignment of a graphs nodes to one of two sets. And as an example here, we have a graph. And Ive decided some vertices are gray and some are white and just totally arbitrary which ones I pick. Second term I want to define is a crossing edge. So a crossing edge is any edge which connects vertices from the gray side to the white side. Now, heres the surprising fact that the cut property tells us. If you make up any cut-- anything you want at all