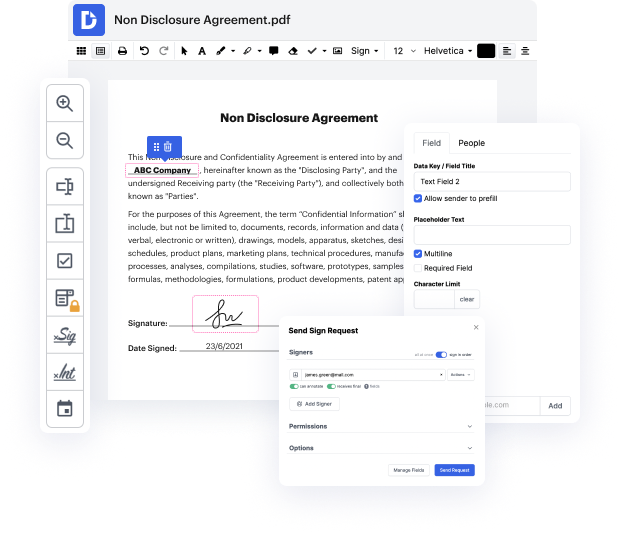
Regardless of how labor-intensive and challenging to edit your files are, DocHub gives an easy way to modify them. You can alter any part in your QUOX without effort. Whether you need to fine-tune a single element or the whole document, you can entrust this task to our robust solution for quick and quality results.
Additionally, it makes sure that the output file is always ready to use so that you’ll be able to get on with your projects without any slowdowns. Our all-encompassing collection of features also includes sophisticated productivity features and a library of templates, enabling you to make best use of your workflows without wasting time on repetitive activities. On top of that, you can gain access to your papers from any device and integrate DocHub with other solutions.
DocHub can handle any of your document management activities. With a great deal of features, you can generate and export documents however you want. Everything you export to DocHub’s editor will be saved safely for as long as you need, with rigid security and data security protocols in place.
Experiment with DocHub now and make handling your files more seamless!
so in this one weamp;#39;re trying to prove that angle abe is going to be congruent to angle a e c d and thereamp;#39;s a couple ways to do this um and it doesnamp;#39;t matter which one you choose to do youamp;#39;re given that you have two different parallelograms this is one of the parallelograms and then this is the other parallelogram and so the the two methods that people would employ on this proof is first you can either prove the two triangles that those angles in are congruent or second you can just use parallel lines iamp;#39;m going to go ahead and do the parallel line method and so youamp;#39;re given that a b f e and b c d e are parallelograms thatamp;#39;s your given notice that youamp;#39;re not given any parallel lines and if you want to use things like for example alternate interior angles which is what weamp;#39;re going to use then you need to claim the parallel lines and so since a b f e is a parallelogram that means a b is parallel to f e and then since b