Not all formats, such as WRI, are developed to be easily edited. Even though many capabilities can help us tweak all document formats, no one has yet created an actual all-size-fits-all tool.
DocHub offers a straightforward and streamlined tool for editing, taking care of, and storing papers in the most popular formats. You don't have to be a technology-savvy user to put in point in WRI or make other changes. DocHub is robust enough to make the process simple for everyone.
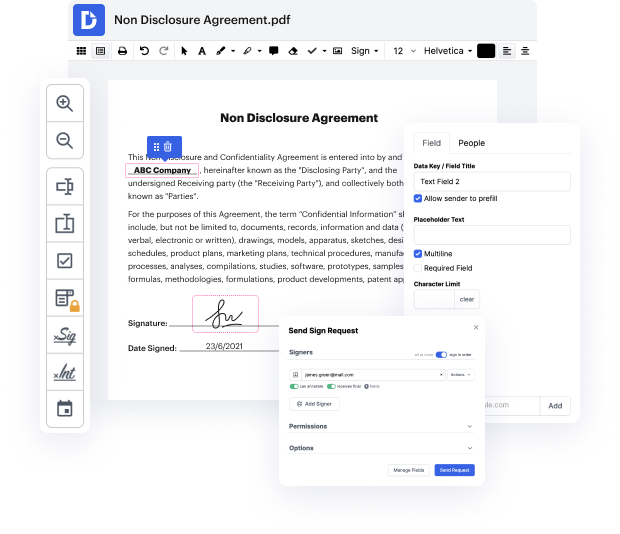
Our tool enables you to alter and tweak papers, send data back and forth, generate interactive forms for information gathering, encrypt and safeguard paperwork, and set up eSignature workflows. In addition, you can also create templates from papers you use on a regular basis.
You’ll locate a great deal of additional tools inside DocHub, such as integrations that allow you to link your WRI document to a wide array of business apps.
DocHub is a straightforward, fairly priced way to handle papers and streamline workflows. It offers a wide range of capabilities, from creation to editing, eSignature solutions, and web form creating. The application can export your documents in many formats while maintaining highest protection and adhering to the greatest information protection criteria.
Give DocHub a go and see just how simple your editing process can be.
welcome so what Iamp;#39;m going to do is show you how to uh write this equation in our slope intercept form by using point slope form so to do that again we need to write out our equation our y - y1 = M * x - X1 and we have a point m in the slope when we know the slope we can put in for M and our point weamp;#39;re going to put in for X1 and y1 so we plug those into our coordinates and you could plug them into X and Y if you want to itamp;#39;s just going to be a little bit extra work for you because then youamp;#39;re going to have a negative y1 which youamp;#39;ll have to undo so we like to always put it in for this so therefore I can just isolate my y value but you can do it either way you want to because these represent X and Y coordinates so they could go in for either coordinate so I have y - 2 = 45s * X - 1 now I need to apply my distributive property so I have y - 2 = 4 4 fths xus 4 fths add two add two now I need to add two to 4 fths so a 4 fths so I have -4 fths plus 2