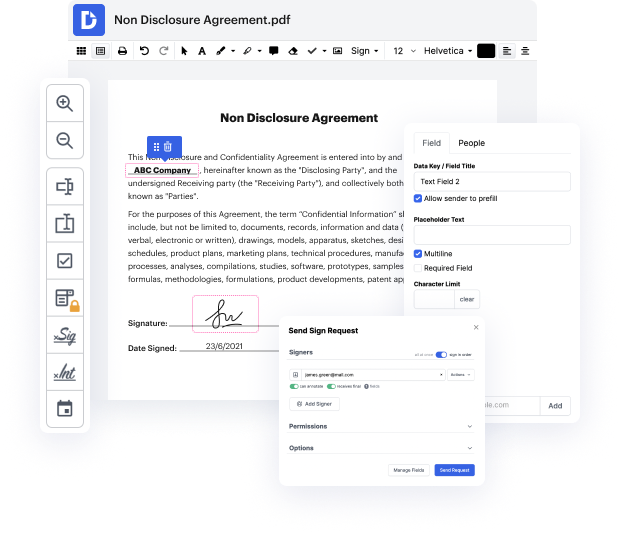
Not all formats, such as PDAX, are designed to be easily edited. Even though a lot of tools can help us modify all form formats, no one has yet invented an actual all-size-fits-all tool.
DocHub gives a simple and streamlined tool for editing, managing, and storing paperwork in the most widely used formats. You don't have to be a tech-knowledgeable person to omit subject in PDAX or make other tweaks. DocHub is robust enough to make the process straightforward for everyone.
Our tool allows you to change and tweak paperwork, send data back and forth, generate interactive documents for data gathering, encrypt and safeguard forms, and set up eSignature workflows. Moreover, you can also generate templates from paperwork you utilize on a regular basis.
You’ll locate a great deal of other functionality inside DocHub, including integrations that allow you to link your PDAX form to different business applications.
DocHub is a straightforward, fairly priced way to handle paperwork and improve workflows. It provides a wide array of features, from creation to editing, eSignature professional services, and web document building. The program can export your paperwork in multiple formats while maintaining maximum safety and following the greatest data protection criteria.
Give DocHub a go and see just how straightforward your editing process can be.
the following content is provided under a Creative Commons license your support will help MIT open courseware continue to offer highquality educational resources for free to make a donation or to view additional materials from hundreds of MIT courses visit MIT open courseware at ocw.mit.edu all right uh today we have lecture guest lecture two of two by C scalak all right uh glad to be back so letamp;#39;s continue on the path we followed last time um let me remind you what we did last time first of all so I talked about uh interesting theorems in topology Nash uh sperner and Brower and I uh you know defined the corresponding so these were theorems in topology I Define the corresponding problems uh and uh because of this existing theorems the corresponding search problems were total and then I looked into the problems in NP that are total and um I tried to identify what what in these problems make them total and try to identify a combinatorial argument that guarantees the existence of