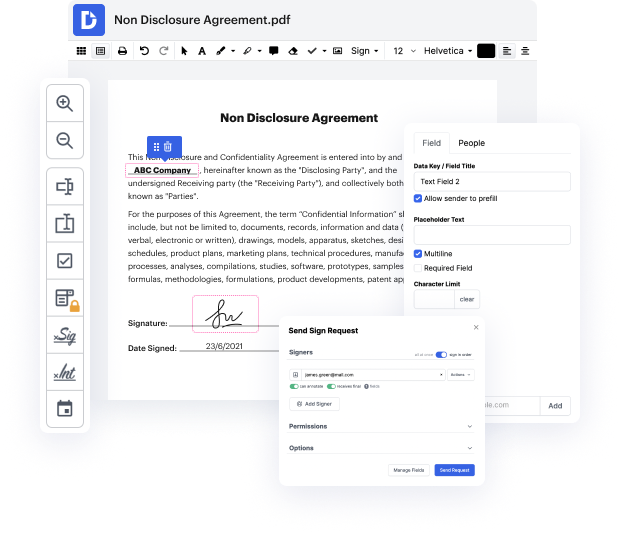
Disadvantages are present in every solution for editing every document type, and even though you can find a lot of solutions on the market, not all of them will suit your specific needs. DocHub makes it much simpler than ever to make and change, and deal with documents - and not just in PDF format.
Every time you need to quickly negate address in aspx, DocHub has got you covered. You can quickly alter document elements such as text and images, and layout. Customize, arrange, and encrypt files, build eSignature workflows, make fillable forms for smooth information collection, and more. Our templates feature enables you to generate templates based on documents with which you often work.
Additionally, you can stay connected to your go-to productivity capabilities and CRM platforms while handling your files.
One of the most extraordinary things about utilizing DocHub is the option to handle document activities of any difficulty, regardless of whether you require a fast tweak or more diligent editing. It includes an all-in-one document editor, website document builder, and workflow-centered capabilities. Additionally, you can rest assured that your documents will be legally binding and adhere to all protection frameworks.
Cut some time off your projects with DocHub's tools that make handling files effortless.
Welcome! In this tutorial, we will solve this maximization problem using graphical method. Lets label the constraints C1 to C4 for reference purposes. Lets start by setting up tables to find the points. The line equation for Constraint 1) is 7X - Y =3 So when X = 0, Y = -3 And when Y = 0, X = 0.43 These two points are not that useful to us because the first has a negative which will take us far away from the feasible region and make the graph very small. The other has a fractional value that cannot be easily located on the graph. So lets try finding more points. To make it easy to find useful points, it is better to rewrite the equation in terms of one variable. In this case, we can write it in terms of Y. That is, Y = 7X - 3. We can now use trial and error to find better points. For example, when X = 0.5, Y also equals 0.5. And when X = 1, Y equals 4. For Constraint 2) we have the line -3x + 6y = 10 when X = 0, Y = 1.67. And when Y = 0, X = -3.33. Again, lets try more points. Rewr