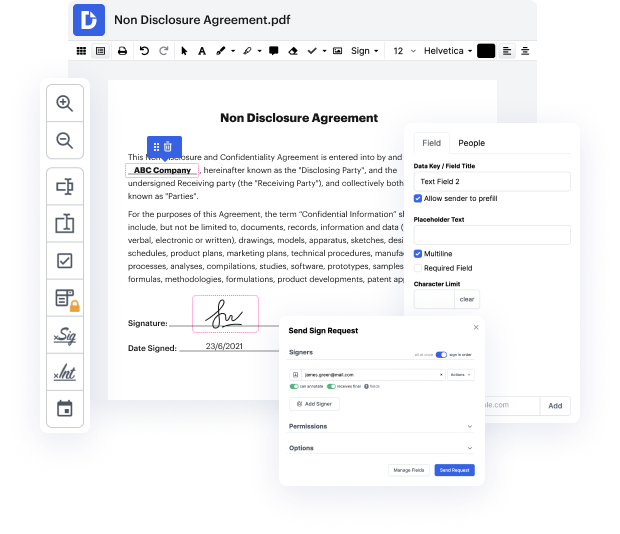
Not all formats, including EZW, are developed to be easily edited. Even though a lot of tools can help us tweak all document formats, no one has yet invented an actual all-size-fits-all solution.
DocHub gives a straightforward and efficient solution for editing, managing, and storing papers in the most popular formats. You don't have to be a tech-knowledgeable user to inlay character in EZW or make other tweaks. DocHub is robust enough to make the process straightforward for everyone.
Our feature enables you to alter and edit papers, send data back and forth, create interactive forms for data gathering, encrypt and protect paperwork, and set up eSignature workflows. Additionally, you can also generate templates from papers you utilize frequently.
You’ll locate plenty of additional tools inside DocHub, including integrations that let you link your EZW document to a wide array of business programs.
DocHub is an intuitive, cost-effective way to handle papers and simplify workflows. It provides a wide range of features, from generation to editing, eSignature providers, and web document developing. The program can export your documents in multiple formats while maintaining maximum security and following the maximum data protection standards.
Give DocHub a go and see just how straightforward your editing process can be.
do covered that ah how to use the discrete wavelet transform in images and then we had also planned to cover that how the dwt coefficients are actually encoded in order to generate the bit stream now ah we could not exactly cover to the extent we had desired in the last class because of ah some shortage of time so we are going to continue with that in this lecture and the title that we have for this lecture is embedded zero tree wavelet encoding now towards the end of the last lecture i had actually introduced to you the concept of the parent child relationship that exists between the coefficients in the different sub bands all right and especially we had seen that whenever we are changing from one resolution to the next okay to the to the more final resolutions whenever we are going there we are finding that ah one pixel or one coefficient in the ah coarser resolution or coarser scale that corresponds to four ah coefficients in the next final level of scale ok and this is what will fo