Not all formats, such as raw, are designed to be effortlessly edited. Even though a lot of capabilities can help us change all document formats, no one has yet created an actual all-size-fits-all solution.
DocHub provides a easy and streamlined solution for editing, handling, and storing paperwork in the most widely used formats. You don't have to be a technology-knowledgeable user to fix chapter in raw or make other tweaks. DocHub is powerful enough to make the process easy for everyone.
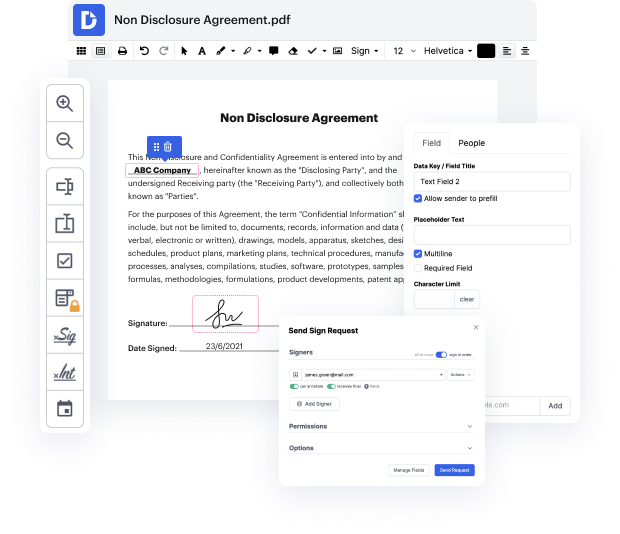
Our tool allows you to change and tweak paperwork, send data back and forth, generate interactive documents for information collection, encrypt and protect paperwork, and set up eSignature workflows. In addition, you can also generate templates from paperwork you use frequently.
You’ll locate a great deal of other features inside DocHub, such as integrations that let you link your raw document to a variety business programs.
DocHub is a simple, cost-effective way to manage paperwork and improve workflows. It offers a wide selection of tools, from generation to editing, eSignature services, and web document creating. The program can export your documents in many formats while maintaining highest protection and following the greatest information security requirements.
Give DocHub a go and see just how easy your editing process can be.
in this lesson weamp;#39;re going to use the gauss jordan elimination to solve a system of equations with three variables so hereamp;#39;s the problem x plus y minus z is equal to seven and then weamp;#39;ll have x minus y plus two z thatamp;#39;s equal to three and then two x plus y plus z is equal to nine now the first thing we need to do is convert this to an augmented matrix so we need to write the coefficients so itamp;#39;s going to be 1 1 negative 1 and then to separate the left side from the right side weamp;#39;re going to use the vertical bar now letamp;#39;s put 7 on the right side and then itamp;#39;s going to be 1 negative 1 2 3 and then 2 1 1 9. now what we need to do is we need to make sure that these three numbers and these three are zeros and then these three numbers which form the main diagonal are ones only and in that form itamp;#39;s going to be in reduced row echelon form and whatever numbers we see here will be the values of x y and z so letamp;#39;s go