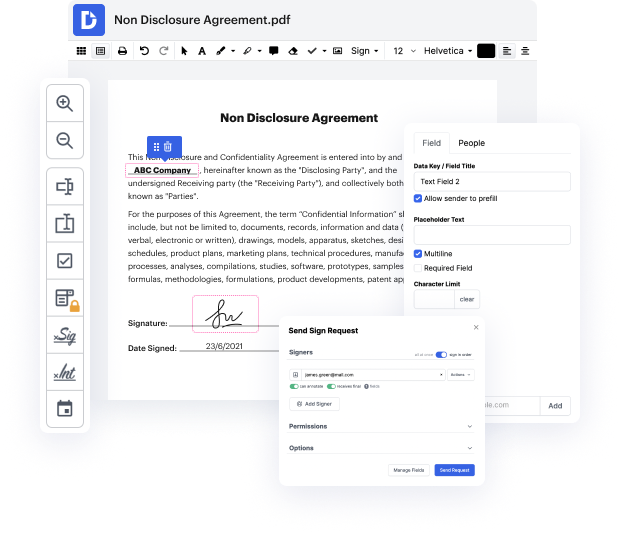
No matter how complex and difficult to edit your documents are, DocHub gives a straightforward way to change them. You can modify any part in your AFP without effort. Whether you need to modify a single element or the whole document, you can entrust this task to our robust tool for fast and quality outcomes.
Moreover, it makes sure that the final document is always ready to use so that you’ll be able to get on with your tasks without any delays. Our extensive group of features also comes with advanced productivity features and a library of templates, enabling you to take full advantage of your workflows without the need of losing time on routine tasks. On top of that, you can access your papers from any device and integrate DocHub with other solutions.
DocHub can handle any of your document management tasks. With an abundance of features, you can create and export documents however you choose. Everything you export to DocHub’s editor will be stored safely as much time as you need, with rigid protection and data protection frameworks in place.
Experiment with DocHub now and make handling your documents more seamless!
So today weamp;#39;re going to be looking at applicative functors which is the second step on our journey towards defining and seeing what monads are but first as usual weamp;#39;re going to have a quick review of what we did last time so what we did last day is we introduced the idea of funs which generalized the idea of mapping to a larger family of data structures so um hereamp;#39;s our old friend the map function which youamp;#39;re all familiar with if youamp;#39;ve done hascal so what map does is it takes a function from A to B and it takes a list of Aamp;#39;s and then itamp;#39;s going to apply the function all the way across the list to give a list of Bamp;#39;s and itamp;#39;s got a simple recursive definition as we see here and the observation we made last day is that the idea of mapping is not specific to the list data structure so working with a list of a to list of B but actually can be generalized to give the idea of whatamp;#39;s called a functor so down at t