Not all formats, such as binary, are developed to be easily edited. Even though a lot of features will let us edit all form formats, no one has yet created an actual all-size-fits-all solution.
DocHub offers a easy and efficient solution for editing, taking care of, and storing papers in the most widely used formats. You don't have to be a technology-savvy person to darken topic in binary or make other modifications. DocHub is powerful enough to make the process simple for everyone.
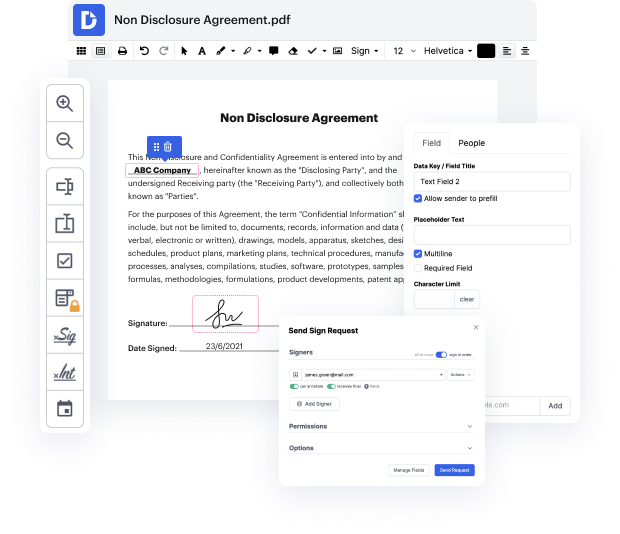
Our feature allows you to modify and edit papers, send data back and forth, generate interactive forms for data gathering, encrypt and safeguard forms, and set up eSignature workflows. Moreover, you can also create templates from papers you use regularly.
You’ll find a great deal of additional tools inside DocHub, including integrations that allow you to link your binary form to various business applications.
DocHub is a simple, fairly priced way to manage papers and streamline workflows. It offers a wide array of capabilities, from generation to editing, eSignature providers, and web form developing. The program can export your paperwork in many formats while maintaining highest protection and adhering to the greatest data security standards.
Give DocHub a go and see just how simple your editing process can be.
if you consider this binary number which Iamp;#39;ve written down here you can see every position is a zero so youamp;#39;re going to have a denory value of zero if you consider this binary number which Iamp;#39;ve written down below you can see here we have one in the four position so all of this is equal to four which Iamp;#39;ve wrote down here and this zero means we have a plus sign which you can see here if we look at this boundary pattern this tells us itamp;#39;s going to be positive the ones in these positions add up to 51 and consequently we can write the binary pattern down like this weamp;#39;ve already seen that this will give us zero if we look at this number we can see weamp;#39;ve got positive and if we add up all of the position coefficients for these numbers we get 127 so we have plus 127 so the range of numbers that can be represented is from zero to Plus 127.