Clear up side in AFP

Use this walkthrough to clear up side in AFP in minutes

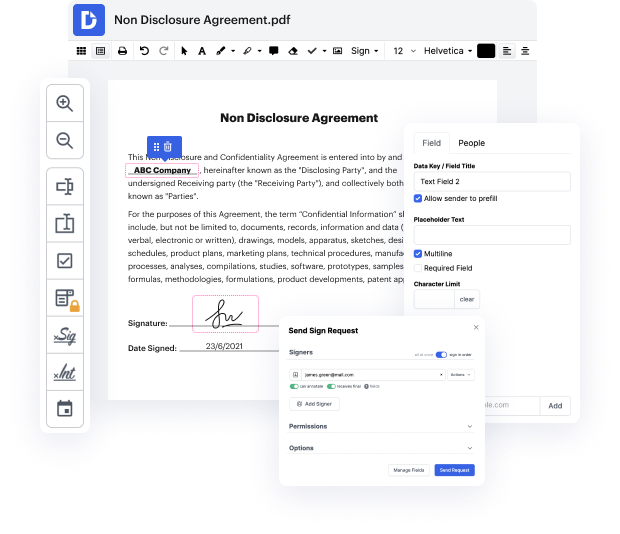
AFP may not always be the simplest with which to work. Even though many editing features are available on the market, not all provide a simple solution. We developed DocHub to make editing easy, no matter the form format. With DocHub, you can quickly and easily clear up side in AFP. Additionally, DocHub gives a range of other functionality including form generation, automation and management, field-compliant eSignature tools, and integrations.

DocHub also lets you save effort by producing form templates from documents that you use regularly. Additionally, you can take advantage of our numerous integrations that allow you to connect our editor to your most used programs effortlessly. Such a solution makes it fast and simple to work with your documents without any slowdowns.

To clear up side in AFP, follow these steps:

Click Log In or register a free account.
When forwarded to your Dashboard, click the Add New button and select how you want to import your form.
Use our advanced features that will let you improve your document's content and design.
Pick the option to clear up side in AFP from the toolbar and apply it to form.
Go over your content once more to ensure it has no mistakes or typos.
Click DONE to complete editing form.

DocHub is a useful feature for individual and corporate use. Not only does it provide a comprehensive collection of features for form generation and editing, and eSignature implementation, but it also has a range of features that prove useful for producing complex and streamlined workflows. Anything imported to our editor is kept safe according to leading field requirements that shield users' data.

Make DocHub your go-to option and streamline your form-based workflows effortlessly!

PDF editing simplified with DocHub

Seamless PDF editing

Editing a PDF is as simple as working in a Word document. You can add text, drawings, highlights, and redact or annotate your document without affecting its quality. No rasterized text or removed fields. Use an online PDF editor to get your perfect document in minutes.

Smooth teamwork

Collaborate on documents with your team using a desktop or mobile device. Let others view, edit, comment on, and sign your documents online. You can also make your form public and share its URL anywhere.

Automatic saving

Every change you make in a document is automatically saved to the cloud and synchronized across all devices in real-time. No need to send new versions of a document or worry about losing information.

Google integrations

DocHub integrates with Google Workspace so you can import, edit, and sign your documents directly from your Gmail, Google Drive, and Dropbox. When finished, export documents to Google Drive or import your Google Address Book and share the document with your contacts.

Powerful PDF tools on your mobile device

Keep your work flowing even when you're away from your computer. DocHub works on mobile just as easily as it does on desktop. Edit, annotate, and sign documents from the convenience of your smartphone or tablet. No need to install the app.

Secure document sharing and storage

Instantly share, email, and fax documents in a secure and compliant way. Set a password, place your documents in encrypted folders, and enable recipient authentication to control who accesses your documents. When completed, keep your documents secure in the cloud.

Drive efficiency with the DocHub add-on for Google Workspace

Access documents and edit, sign, and share them straight from your favorite Google Apps.

Install now

How to clear up side in AFP

5 out of 5

12 votes

so last time around we looked to see how induction can be used not just as a proof technique but also as a technique for constructing programs and we Illustrated this by means of an example we saw how the idea of so-called constructive induction could be used to obtain a fast version of the standard function which reverses a list so what weamp;#39;re going to do today is weamp;#39;re going to kick things off with a quick review of what we did last time around and then weamp;#39;re going to be doing two things first of all weamp;#39;re going to be doing a second example of constructive induction weamp;#39;ll be seeing how it can be used to obtain a fast version of a function which flattens a tree and then secondly weamp;#39;re going to be looking at the final case study which weamp;#39;re going to have in the course which is a compiler correctness result so here is a quick summary of what we achieved in the last lecture so what we have in the top red box is the standard recursive

Related features

Convert Travel Booking Form to Fillable PDF

Convert Travel Booking Form to PPT

Convert Travel Booking Form to Word

Create a PDF Travel Booking Form Template

Travel Booking Form - Create Signing Links with Link2Fill

Travel Booking Form - Create Signing Links with DocHub

E-Sign with DocHub your Travel Booking Form

Send Travel Booking Form to Sign

Got questions?

Below are some common questions from our customers that may provide you with the answer you're looking for. If you can't find an answer to your question, please don't hesitate to reach out to us.

Contact us

What AFP levels indicate Down syndrome?

Alpha Fetoprotein (AFP) Quad Screen, Penta Screen, Test Summary DisorderNormal Screen

How to read AFP test results?

AFP is measured in nanograms per milliliter (ng/mL), with normal levels less than 20 ng/mL. Levels above 400 ng/mL may indicate a liver tumor or other cancer. Elevated levels of AFP may indicate cancer of the liver, ovaries or testicles, but that isnt always the case.

What is a normal AFP level in amniotic fluid?

Maternal serum AFP levels rise from the normal non-pregnancy level of 0.20 ng/mL to about 250 ng/mL at 32 weeks gestation. If the fetus has an open neural tube defect, AFP is thought to leak directly into the amniotic fluid, causing unexpectedly high concentrations of AFP.

How can AFP be reduced?

Iron reduction therapy by phlebotomy alone or in combination with a low-iron diet is an inexpensive treatment with few side effects and may reduce the risk of hepatocarcinogenesis associated with HCV [18]. A few studies have shown that phlebotomy can reduce serum AFP levels in patients with chronic hepatitis C [3436].

What level of AFP indicates cirrhosis?

The study by Harada T, et al. [39] showed that approximately 40% of all cirrhotic patients will have AFP levels higher than 20 ng/ml. An increase in AFP levels (between 10 and 500 ng/ml, and sometimes up to 1000 ng/ml) can be seen in adult patients with hepatitis or cirrhosis with any etiology.

What does an elevated AFP indicate?

AFP in non-pregnant people is mainly measured as a tumor marker. Tumor markers are substances that are often made by cancer cells or by normal cells in response to cancer. High levels of AFP can be a sign of cancer of the liver, ovaries or testicles.

How do I read my AFP pregnancy results?

A positive test with a high AFP suggests a birth defect like spina bifida. Thats typically a result of 2.5 times or more than the average level of AFP youd expect to see at that point in your pregnancy. A positive test with low AFP could mean a problem like Down syndrome or Edwards syndrome.

What is a positive AFP result?

A positive AFP PLUS test means that you are in a higher likelihood group for having a baby with a neural tube defect or a chromosome abnormality. However, it does not prove by itself that there is anything wrong with the pregnancy.

See why our customers choose DocHub

Great solution for PDF docs with very little pre-knowledge required.

"Simplicity, familiarity with the menu and user-friendly. It's easy to navigate, make changes and edit whatever you may need. Because it's used alongside Google, the document is always saved, so you don't have to worry about it."

Pam Driscoll F
Teacher

A Valuable Document Signer for Small Businesses.

"I love that DocHub is incredibly affordable and customizable. It truly does everything I need it to do, without a large price tag like some of its more well known competitors. I am able to send secure documents directly to me clients emails and via in real time when they are viewing and making alterations to a document."

Jiovany A
Small-Business

I can create refillable copies for the templates that I select and then I can publish those.

"I like to work and organize my work in the appropriate way to meet and even exceed the demands that are made daily in the office, so I enjoy working with PDF files, I think they are more professional and versatile, they allow..."

Victoria G
Small-Business

be ready to get more

Edit and sign PDFfor free

Get started now