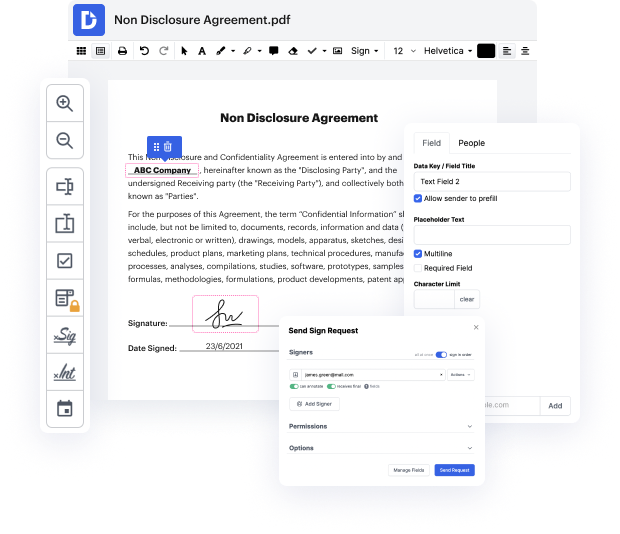
DocHub provides a effortless and user-friendly solution to bold dot in your Product Evaluation. No matter the intricacies and format of your document, DocHub has everything you need to ensure a simple and headache-free modifying experience. Unlike other services, DocHub shines out for its outstanding robustness and user-friendliness.
DocHub is a web-based solution allowing you to change your Product Evaluation from the convenience of your browser without needing software downloads. Owing to its simple drag and drop editor, the ability to bold dot in your Product Evaluation is fast and simple. With multi-function integration capabilities, DocHub allows you to transfer, export, and alter papers from your preferred program. Your completed document will be saved in the cloud so you can access it readily and keep it safe. Additionally, you can download it to your hard drive or share it with others with a few clicks. Alternatively, you can turn your form into a template that prevents you from repeating the same edits, such as the ability to bold dot in your Product Evaluation.
Your edited document will be available in the MY DOCS folder inside your DocHub account. Additionally, you can utilize our editor panel on right-hand side to merge, divide, and convert documents and rearrange pages within your papers.
DocHub simplifies your document workflow by providing an incorporated solution!
in this lesson were going to focus on the dot product which is one of two ways to multiply two vectors together the difference between the dot product and the cross product which is the other way is that the dot product it gives you a scalar quantity after multiplying two vectors the result of the cross product on the other hand is a vector quantity so lets work out an example but first let me give you the formula so lets say if we have vector a with its x component and its y component and vector b with its x and y components the dot product of a and b is simply the product of the x components plus the product of the y components so its a x times bx plus ay times by and thats how you could find the dot product between two vectors so lets try an example so lets say vector a is two comma three and b is five comma negative four go ahead and calculate the dot product of these two vectors feel free to pause the video if you want to so the first thing were going to do is multiply the