Black out index in binary

Your reliable solution to black out index in binary, no downloads required

Not all formats, including binary, are designed to be quickly edited. Even though many tools can help us edit all file formats, no one has yet invented an actual all-size-fits-all tool.

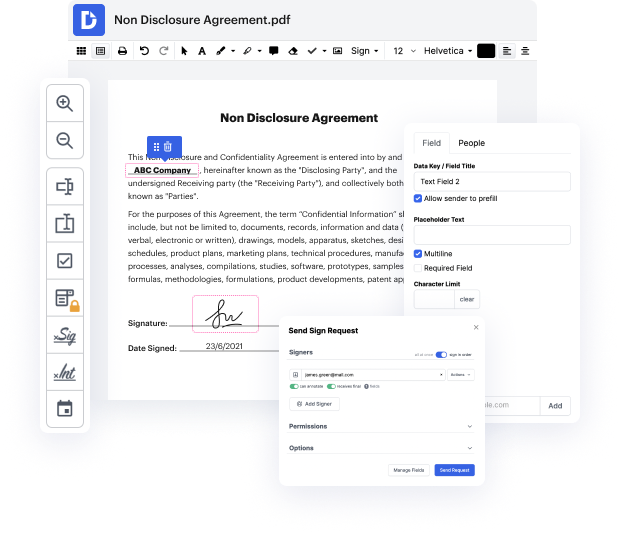
DocHub offers a easy and efficient tool for editing, managing, and storing paperwork in the most widely used formats. You don't have to be a technology-knowledgeable person to black out index in binary or make other modifications. DocHub is robust enough to make the process easy for everyone.

Our feature allows you to alter and tweak paperwork, send data back and forth, create dynamic documents for data gathering, encrypt and safeguard forms, and set up eSignature workflows. In addition, you can also create templates from paperwork you utilize frequently.

You’ll locate plenty of other functionality inside DocHub, including integrations that let you link your binary file to a variety productivity apps.

How to black out index in binary

Head to DocHub’s main page and click Log In.
Import your file to the editor utilizing one of the numerous import options.
Use different tools to get the most out of our editor. In the menu bar, pick the ability to black out index in binary.
Verify text in your form for errors and typos and make sure it looks web-optimized.
After finalizing the editing process, click DONE.
Select what you need to do with the form next: rearrange it, share it as a link, fax it, etc.

DocHub is a straightforward, fairly priced option to handle paperwork and streamline workflows. It offers a wide array of tools, from generation to editing, eSignature professional services, and web document creating. The software can export your files in multiple formats while maintaining maximum protection and adhering to the highest data protection criteria.

Give DocHub a go and see just how easy your editing transaction can be.

PDF editing simplified with DocHub

Seamless PDF editing

Editing a PDF is as simple as working in a Word document. You can add text, drawings, highlights, and redact or annotate your document without affecting its quality. No rasterized text or removed fields. Use an online PDF editor to get your perfect document in minutes.

Smooth teamwork

Collaborate on documents with your team using a desktop or mobile device. Let others view, edit, comment on, and sign your documents online. You can also make your form public and share its URL anywhere.

Automatic saving

Every change you make in a document is automatically saved to the cloud and synchronized across all devices in real-time. No need to send new versions of a document or worry about losing information.

Google integrations

DocHub integrates with Google Workspace so you can import, edit, and sign your documents directly from your Gmail, Google Drive, and Dropbox. When finished, export documents to Google Drive or import your Google Address Book and share the document with your contacts.

Powerful PDF tools on your mobile device

Keep your work flowing even when you're away from your computer. DocHub works on mobile just as easily as it does on desktop. Edit, annotate, and sign documents from the convenience of your smartphone or tablet. No need to install the app.

Secure document sharing and storage

Instantly share, email, and fax documents in a secure and compliant way. Set a password, place your documents in encrypted folders, and enable recipient authentication to control who accesses your documents. When completed, keep your documents secure in the cloud.

Drive efficiency with the DocHub add-on for Google Workspace

Access documents and edit, sign, and share them straight from your favorite Google Apps.

Install now

How to black out index in binary

5 out of 5

17 votes

When deciding how to store large amounts of data, a key question is how to organize that data so that we can operate on it efficiently. Letamp;#39;s start by looking at a popular data structure, the binary search tree. A binary search tree consists of connected nodes. Each node has a key, in this case a unique number, and can point to a left child node and a right child node. Binary search trees obey the property that any keys to the left of a node are less than that nodeamp;#39;s key, and any keys to the right of a node are greater than that nodeamp;#39;s key. This allows for an efficient search process. If we want to search for a key, we start at the root of the tree and compare against the key there, going left or right depending on if the key we want is less than or greater than the key in the node. At each step, we pick only the half of the tree that might contain the key weamp;#39;re looking for, saving time by not bothering to search parts of the tre

Got questions?

Below are some common questions from our customers that may provide you with the answer you're looking for. If you can't find an answer to your question, please don't hesitate to reach out to us.

Contact us

What are indices in binary trading?

Stock market indices measure the value of a section of the stock market, via a weighted average of selected stocks from particular companies. These companies are usually selected from a certain industry or market sector. Its very important to note that there are various stock indices that serve different purposes.

What is the Fenwick tree concept?

A Fenwick tree is actually three implicit trees over the same array: the interrogation tree used for translating indexes to prefix sums, the update tree used for updating elements, and the search tree for translating prefix sums to indexes (rank queries). Fenwick tree - Wikipedia Wikipedia wiki Fenwicktree Wikipedia wiki Fenwicktree

What is an index in coding?

An index picks out a specific value from a list or a specific character from a string. But we can also pick out several values to a new list or string. We do this by specifiying two indexes, a start- and end-index. s = Yes, Python is a language. language = s[5:11] print(language) # prints Python Copy code.

Is the binary tree complete?

Complete Binary Tree: This is a tree in which all levels are fully filled, except for possibly the last level, which is filled from left to right. Its useful for improving storage optimization because it ensures that each level is filled entirely before populating the next. Full vs. Complete Binary Tree: Whats the Difference? | Built In Built In data-science full-tree Built In data-science full-tree

What is index in binary?

Note: Indexing in the binary representation starts from 0 from the right. For example in the binary number 000011, the first set bit is at index 0 from the right, and the second set bit is at index 1 from the right. Examples: Input: N = 15, K = 3 Output: 2 15 is 1111, hence the third bit is at index 2 from right. Position of the K-th set bit in a number - GeeksforGeeks GeeksforGeeks position-of-the-k-th-set GeeksforGeeks position-of-the-k-th-set

How to index a BST?

An indexed BST is derived from a BST by adding a field, LeftSize, to each tree node, whose value is the number of nodes in its left- subtree plus 1. Since the number of nodes, as well as its shape, will change frequently, it is appropriate to use a linked structure to represent a binary search tree. Binary Search Trees, etc. plymouth.edu Webfiles notes note11 plymouth.edu Webfiles notes note11

What is index in binary tree?

Finding out the index of a number within a binary tree is a common task and involves references to its left and right child. The term index in the node typically refers to a position of a node within the tree that allows for efficient navigation and access to specified nodes.

How to find an index in binary search?

The Algorithm Calculate the middle element index: mid = start + (end - start) / 2 . Compare the value at middle index ( mid ) with the target value. If arr[mid] is equal to the target value, return mid (search successful). If arr[mid] is less than the target value, set the start to mid + 1 .

How to calculate index in binary tree?

For instance, to get the child nodes of the node with 8 as its value and 3 as its index, the left child node index would be 2 x 3 + 1, which is index 7 (node value is 6). The right child node index is 2 x 3 + 2, which is index 8 (node value is 0). The parent node index can be calculated by floor((index - 1) / 2).

How to construct a BST?

Algorithm Create the root node as NULL initially. Traverse the level order traversal array and for each of its elements, insert the node corresponding to it in the BST. There are three conditions encountered when a new node is to be inserted in the BST at any level. Finally, print the preorder traversal of the BST.

See why our customers choose DocHub

Great solution for PDF docs with very little pre-knowledge required.

"Simplicity, familiarity with the menu and user-friendly. It's easy to navigate, make changes and edit whatever you may need. Because it's used alongside Google, the document is always saved, so you don't have to worry about it."

Pam Driscoll F
Teacher

A Valuable Document Signer for Small Businesses.

"I love that DocHub is incredibly affordable and customizable. It truly does everything I need it to do, without a large price tag like some of its more well known competitors. I am able to send secure documents directly to me clients emails and via in real time when they are viewing and making alterations to a document."

Jiovany A
Small-Business

I can create refillable copies for the templates that I select and then I can publish those.

"I like to work and organize my work in the appropriate way to meet and even exceed the demands that are made daily in the office, so I enjoy working with PDF files, I think they are more professional and versatile, they allow..."

Victoria G
Small-Business

be ready to get more

Edit and sign PDFfor free

Get started now

Your reliable solution to black out index in binary, no downloads required

How to black out index in binary

PDF editing simplified with DocHub

Drive efficiency with the DocHub add-on for Google Workspace

How to black out index in binary

Got questions?

What are indices in binary trading?

What is the Fenwick tree concept?

What is an index in coding?

Is the binary tree complete?

What is index in binary?

How to index a BST?

What is index in binary tree?

How to find an index in binary search?

How to calculate index in binary tree?

How to construct a BST?

See why our customers choose DocHub

Edit and sign PDFfor free

Try more PDF tools