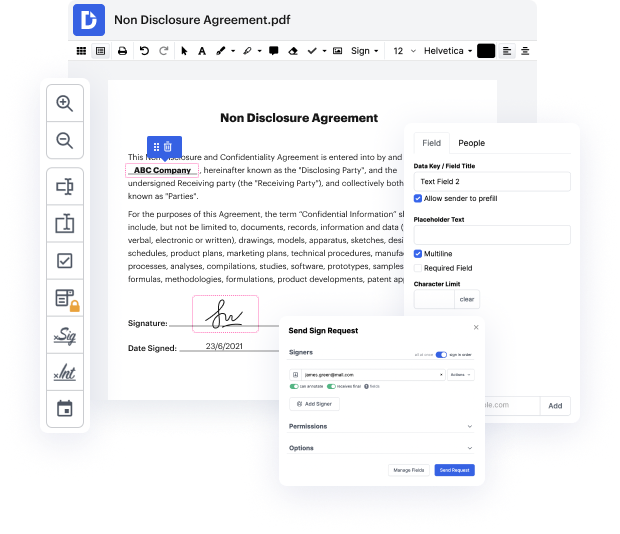
Regardless of how labor-intensive and hard to edit your documents are, DocHub delivers a simple way to change them. You can modify any part in your jpeg with no effort. Whether you need to fine-tune a single component or the whole form, you can rely on our powerful solution for quick and quality results.
Additionally, it makes certain that the final file is always ready to use so that you’ll be able to get on with your tasks without any slowdowns. Our all-encompassing set of capabilities also comes with pro productivity features and a library of templates, allowing you to take full advantage of your workflows without wasting time on recurring tasks. In addition, you can gain access to your documents from any device and integrate DocHub with other solutions.
DocHub can take care of any of your form management tasks. With a great deal of capabilities, you can generate and export paperwork however you choose. Everything you export to DocHub’s editor will be saved safely for as long as you need, with rigid protection and data protection frameworks in place.
Check DocHub now and make managing your files easier!
In the last video, we talked about the beginnings of JPEG, so what do we do at the beginning of the process to start preparing for the discrete cosine transform, which is really how the lossy compression happens within a JPEG. We start with our RGB image, we convert that into YCbCr color space, which separates illuminance and chrominance. And then we can down sample the chrominance if we want, and we can kind of get away with quite a bit of down sampling there that people wonamp;#39;t be able to see. The next step is the discrete cosine transform. Before we start talking about how images are compressed using the discrete cosine transform, itamp;#39;s much better just to start with a simple example of what a discrete cosine transform is and how it works. A cosine function, for anyone who isnamp;#39;t familiar with it, is a function that goes between 1 and -1. What we tend to do on this x-axis is go from 0, to pi, to 2*pi. This is in radians, those of you familiar with degrees, this i