Fill in type in binary

Fill in type in binary with our multi-purpose editing tool

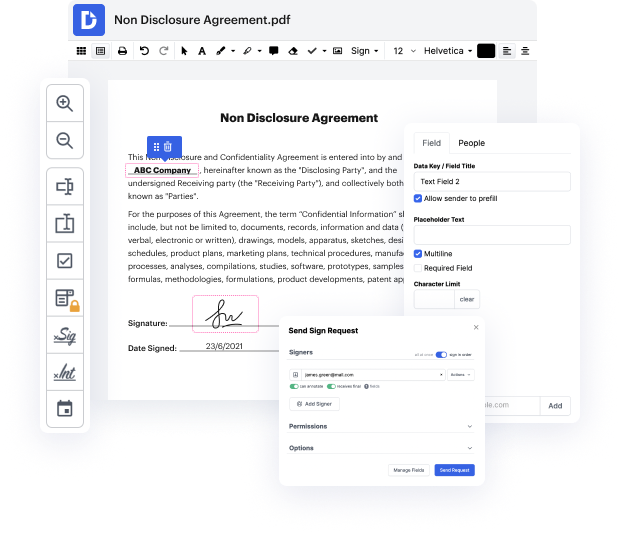
No matter how labor-intensive and challenging to edit your documents are, DocHub delivers a simple way to change them. You can modify any part in your binary without effort. Whether you need to tweak a single component or the whole form, you can rely on our powerful tool for fast and quality outcomes.

In addition, it makes sure that the output form is always ready to use so that you’ll be able to get on with your tasks without any slowdowns. Our extensive set of tools also comes with advanced productivity features and a collection of templates, enabling you to make the most of your workflows without wasting time on repetitive operations. Moreover, you can access your papers from any device and incorporate DocHub with other solutions.

How to fill in type in binary

Start by hitting our free trial option or logging in to your existing account.
Import your form to DocHub’s editor.
Take a look at DocHub’s features and locate the option to fill in type in binary.
Go over your form for any typos or errors.
Select DONE to use changes. Use any delivery option and other tools for arranging your papers.

DocHub can take care of any of your form management operations. With an abundance of tools, you can create and export papers however you want. Everything you export to DocHub’s editor will be stored safely as much time as you need, with rigid safety and data protection frameworks in place.

Experiment with DocHub today and make handling your documents more seamless!

PDF editing simplified with DocHub

Seamless PDF editing

Editing a PDF is as simple as working in a Word document. You can add text, drawings, highlights, and redact or annotate your document without affecting its quality. No rasterized text or removed fields. Use an online PDF editor to get your perfect document in minutes.

Smooth teamwork

Collaborate on documents with your team using a desktop or mobile device. Let others view, edit, comment on, and sign your documents online. You can also make your form public and share its URL anywhere.

Automatic saving

Every change you make in a document is automatically saved to the cloud and synchronized across all devices in real-time. No need to send new versions of a document or worry about losing information.

Google integrations

DocHub integrates with Google Workspace so you can import, edit, and sign your documents directly from your Gmail, Google Drive, and Dropbox. When finished, export documents to Google Drive or import your Google Address Book and share the document with your contacts.

Powerful PDF tools on your mobile device

Keep your work flowing even when you're away from your computer. DocHub works on mobile just as easily as it does on desktop. Edit, annotate, and sign documents from the convenience of your smartphone or tablet. No need to install the app.

Secure document sharing and storage

Instantly share, email, and fax documents in a secure and compliant way. Set a password, place your documents in encrypted folders, and enable recipient authentication to control who accesses your documents. When completed, keep your documents secure in the cloud.

Drive efficiency with the DocHub add-on for Google Workspace

Access documents and edit, sign, and share them straight from your favorite Google Apps.

Install now

How to fill in type in binary

4.9 out of 5

48 votes

okay so good day to all of you so in this video tutorial iamp;#39;m going to teach you how to create a binary search tree but before we go with our example so binary search tree okay binary search three so in simplest form the binary search three is composed of a parent node and this parent node can hold a maximum number of two child nodes so for these two child nodes on the left side the value of the child node must be less than the parent node while the value of the child node node of the right side should be greater than the parent node so that that is the principle of our binary search tree so how are we going to apply for example if weamp;#39;re given a pre-ordered list of elements and then weamp;#39;re going to create a binary search tree out of that so letamp;#39;s have the first example so we have example one so the following sequence of numbers is we have five ten four two 16 7 1 20 15 and 3 okay so our first element is five so that will be our first node so letamp;#39;s

Got questions?

Below are some common questions from our customers that may provide you with the answer you're looking for. If you can't find an answer to your question, please don't hesitate to reach out to us.

Contact us

What is binary typing?

Binary is a numeric system that is comprised of digits zero and one. A computer uses these digits to place data within the computer. The digits can represent letters used to convey important messages.

How do you type in binary?

Uppercase letters start with 010 and lowercase letters start with 011. The letter a is 01100001. From there, count the number of the letter and write that number in binary. For example, the letter d is the fourth letter (100), which is written as 01100100 in binary.

How do you represent letters in binary?

Binary numbers are converted into letters using the American Society for Information Interchange codes. Each letter consists of eight numbers. Uppercase letters start with 010 and lowercase letters start with 011. The letter a is 01100001. Binary Letters: A Guide to Breaking the Code | Built In Built In articles binary-letters Built In articles binary-letters

How can we write in binary?

0:57 3:54 Two is bigger than one. So we put a zero to show that we will not use any twos. Now we can use a oneMoreTwo is bigger than one. So we put a zero to show that we will not use any twos. Now we can use a one. So that one minus one equals zero. Once we get to zero we are complete. How to Write Numbers in Binary - YouTube YouTube watch YouTube watch

How do we represent text in binary?

The ASCII code takes each character on the keyboard and assigns it a binary number. For example: the letter a has the binary number 0110 0001 (this is the denary number 97) the letter b has the binary number 0110 0010 (this is the denary number 98)

How do we represent in binary?

A binary number system is one of the four types of number system. In computer applications, where binary numbers are represented by only two symbols or digits, i.e. 0 (zero) and 1(one). The binary numbers here are expressed in the base-2 numeral system. For example, (101)2 is a binary number. Binary Number System - Definition, Conversion and Examples - BYJUS BYJUS maths binary-number-system BYJUS maths binary-number-system

Why is a in binary 01000001?

The capital letter A is represented by the number 65 in the ASCII code (65 is 01000001 in binary). The first 65 ASCII codes (0 through 64) are used for an assortment of Control characters and special characters, so capital A ended up at 65. Capital B is 66 (01000010) and so on.

How is text represented in binary?

The representation for each character is simply its number converted to a 32 bit binary number. Leading zeroes are used if there are not enough bits (just like how you can represent 254 as a 4 digit decimal number 0254). Data Representation 5.4. Text - Computer Science Field Guide Computer Science Field Guide chapters text Computer Science Field Guide chapters text

See why our customers choose DocHub

Great solution for PDF docs with very little pre-knowledge required.

"Simplicity, familiarity with the menu and user-friendly. It's easy to navigate, make changes and edit whatever you may need. Because it's used alongside Google, the document is always saved, so you don't have to worry about it."

Pam Driscoll F
Teacher

A Valuable Document Signer for Small Businesses.

"I love that DocHub is incredibly affordable and customizable. It truly does everything I need it to do, without a large price tag like some of its more well known competitors. I am able to send secure documents directly to me clients emails and via in real time when they are viewing and making alterations to a document."

Jiovany A
Small-Business

I can create refillable copies for the templates that I select and then I can publish those.

"I like to work and organize my work in the appropriate way to meet and even exceed the demands that are made daily in the office, so I enjoy working with PDF files, I think they are more professional and versatile, they allow..."

Victoria G
Small-Business

be ready to get more

Edit and sign PDFfor free

Get started now

Fill in type in binary with our multi-purpose editing tool

How to fill in type in binary

PDF editing simplified with DocHub

Drive efficiency with the DocHub add-on for Google Workspace

How to fill in type in binary

Got questions?

What is binary typing?

How do you type in binary?

How do you represent letters in binary?

How can we write in binary?

How do we represent text in binary?

How do we represent in binary?

Why is a in binary 01000001?

How is text represented in binary?

See why our customers choose DocHub

Edit and sign PDFfor free

Try more PDF tools