Not all formats, such as binary, are designed to be quickly edited. Even though numerous capabilities will let us change all document formats, no one has yet created an actual all-size-fits-all solution.
DocHub provides a straightforward and streamlined solution for editing, taking care of, and storing documents in the most widely used formats. You don't have to be a tech-knowledgeable user to erase trait in binary or make other modifications. DocHub is robust enough to make the process easy for everyone.
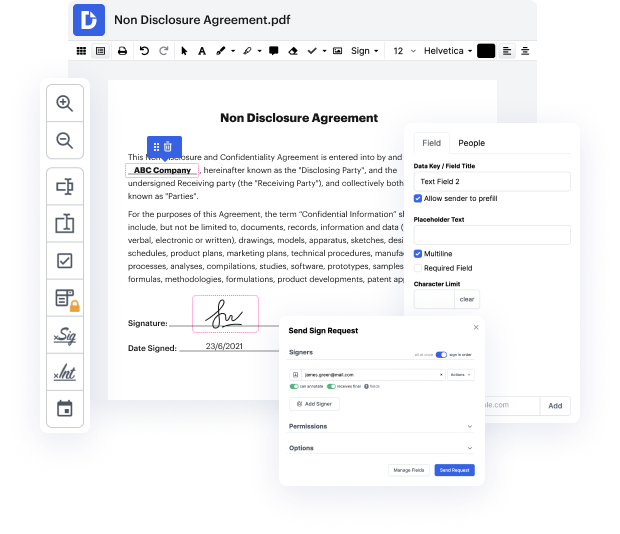
Our feature allows you to change and tweak documents, send data back and forth, create interactive forms for information gathering, encrypt and shield forms, and set up eSignature workflows. Moreover, you can also generate templates from documents you use frequently.
You’ll find a great deal of additional tools inside DocHub, including integrations that let you link your binary document to a wide array of productivity apps.
DocHub is an intuitive, cost-effective way to deal with documents and improve workflows. It provides a wide range of tools, from creation to editing, eSignature solutions, and web document creating. The application can export your documents in many formats while maintaining highest protection and adhering to the highest information safety criteria.
Give DocHub a go and see just how easy your editing process can be.
all right now that we know how to insert elements into a binary search tree we might also want to remove elements from a binary search tree and this is slightly more complicated but Iamp;#39;m going to make it very simple for you guys so when we removing elements from a binary search tree you can think of it as a two-step process first we have to find the element we wish to remove within the binary search tree if it exists at all and in the second stage we want to replace the node weamp;#39;re removing with its successor if one exists in order to maintain the binary search tree invariance now let me remind you where the binary search tree invariant is itamp;#39;s that the left subtree has smaller elements than the current node and the right subtree has larger elements than they carry node okay so letamp;#39;s dive into phase one the fine phase so if weamp;#39;re searching for an element inside our binary search tree one of four things is going to happen the first thing is we hit a