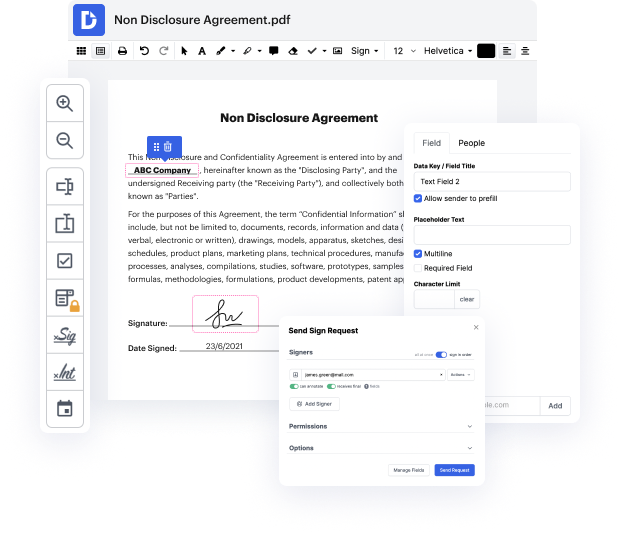
Cuando editas archivos en diferentes formatos todos los días, la universalidad de las herramientas de documentos importa mucho. Si tus instrumentos solo funcionan para algunos de los formatos populares, puedes encontrarte cambiando entre ventanas de software para trabajar en campo en binario y manejar otros formatos de documentos. Si deseas quitarte el dolor de cabeza de la edición de documentos, obtén una solución que pueda gestionar fácilmente cualquier extensión.
Con DocHub, no necesitas concentrarte en nada más que en la edición real de documentos. No tendrás que malabarear aplicaciones para trabajar con diferentes formatos. Te ayudará a editar tu binario tan fácilmente como cualquier otra extensión. Crea documentos binarios, modifícalos y compártelos en una única solución de edición en línea que te ahorra tiempo y aumenta tu eficiencia. Todo lo que tienes que hacer es registrarte en una cuenta en DocHub, lo cual toma solo unos minutos.
No necesitarás convertirte en un multitarea de edición con DocHub. Su conjunto de características es suficiente para una edición rápida de documentos, independientemente del formato que desees revisar. Comienza registrando una cuenta y ve lo fácil que puede ser la gestión de documentos teniendo una herramienta diseñada específicamente para satisfacer tus necesidades.
hola y bienvenidos a esta serie de conferencias sobre campos finitos para la codificación de control mi nombre es Damita Marcia Bay y hoy vamos a discutir sobre el campo binario está bien pero antes de discutir el campo binario revisemos rápidamente algunos de los conceptos que hemos aprendido o básicamente la definición del campo está bien un campo es básicamente un triplete conjunto junto con las dos operaciones adición y multiplicación si y solo si satisface ciertas condiciones y la primera de esas condiciones es que la multiplicación debe ser distributiva sobre la adición lo que significa que para todos los elementos ABC de s a por B más C debe ser igual a a por B más a por C aparte de esta condición este conjunto F bajo multiplicación debe ser un grupo conmutativo por lo que debe satisfacer cierre ley asociativa identidad inversa así como conmutatividad ahora el elemento no cero de este conjunto F bajo multiplicación también debe formar un grupo conmutativo por lo que debe satisfacer el elemento no cero del conjunto F así que para satisfacer cierre a