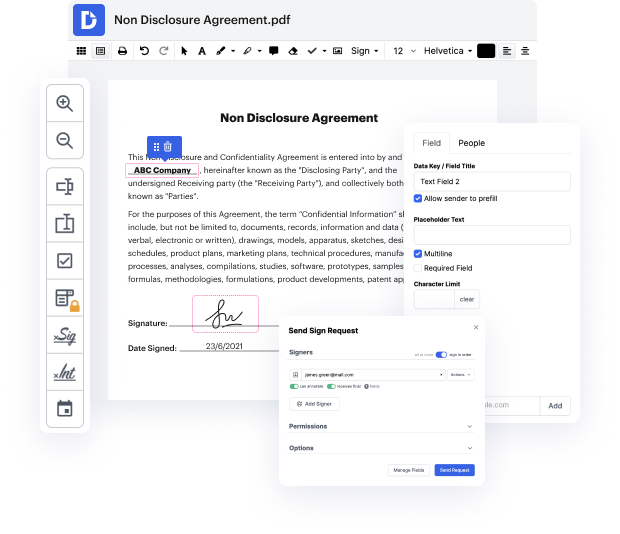
La generación y aprobación de documentos son componentes centrales de sus flujos de trabajo diarios. Estas operaciones son frecuentemente repetitivas y que consumen mucho tiempo, lo que influye en sus equipos y departamentos. Específicamente, la creación, almacenamiento y ubicación de peticiones son importantes para asegurar la eficiencia de su empresa. Una solución en línea completa puede resolver una serie de problemas vitales relacionados con el rendimiento de sus equipos y la gestión de documentos: elimina tareas tediosas, facilita la localización de archivos y la recolección de firmas, y conduce a informes y análisis mucho más precisos. Ahí es cuando puede necesitar una plataforma robusta y multifuncional como DocHub para manejar estas tareas de manera rápida y segura.
DocHub le permite simplificar incluso su proceso más complejo con sus funciones y funcionalidades robustas. Un potente editor de PDF y eSignature mejoran su gestión diaria de documentos y la convierten en un asunto de varios clics. Con DocHub, no necesitará buscar soluciones de terceros adicionales para completar su ciclo de generación y aprobación de documentos. Una interfaz fácil de usar le permite comenzar a trabajar con la petición de inmediato.
DocHub es más que simplemente un editor de PDF en línea y software de eSignature. Es una plataforma que le ayuda a simplificar sus flujos de trabajo de documentos e integrarlos con soluciones de almacenamiento en la nube populares como Google Drive o Dropbox. Pruebe modificar la petición de inmediato y explore el vasto conjunto de funciones y funcionalidades de DocHub.
Comience su prueba gratuita de DocHub ahora mismo, sin tarifas ocultas y sin compromiso. Descubra todas las funciones y opciones de una gestión de documentos fácil y bien hecha. Complete la petición, obtenga firmas y mejore sus flujos de trabajo en su aplicación para smartphone o versión de escritorio sin sudar. Mejore todas sus tareas diarias con la mejor solución disponible en el mercado.
aquí vamos a ver la noción de un conjunto de índices y las intersecciones y uniones sobre conjuntos indexados así que veamos la definición así que queremos comenzar con i donde eso es cualquier conjunto y realmente quiero decir cualquier conjunto aquí hay algunas elecciones generalmente estándar para conjuntos de índices pero realmente puedes tomarlo como arbitrario pero la única regla que necesitas es que para todo pequeño i y grande I podemos producir algún conjunto a sub i y luego queríamos encontrar la unión sobre todos estos conjuntos y la intersección sobre todos estos conjuntos así que la unión sobre los ai a medida que i corre desde este conjunto de índices grande I así que eso va a ser todo x que satisface esta regla así que x está en aj para al menos un j y i así que puedes pensar en esto como una declaración de al menos uno como si fuera una declaración o y luego a continuación la intersección de los a i sobre este conjunto de índices es todo x que satisface esta regla así que x está en aj para todos j y i así que aquí puedes pensar en esto para todos como si fuera una declaración y si quieres relacionar th
