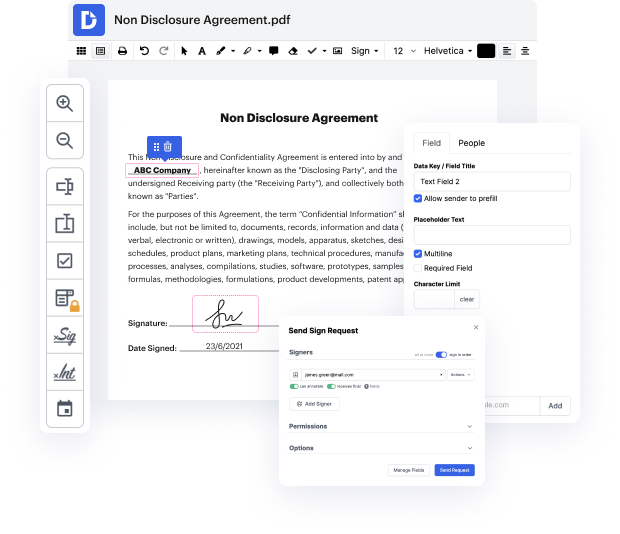
La creación de documentos es un elemento esencial de la comunicación y gestión organizacional efectiva. Necesitas una solución rentable y funcional sin importar tu punto de preparación de documentos. La preparación de permisos puede ser una de esas operaciones que requieren cuidado y consideración adicionales. En términos simples, encontrarás mejores posibilidades que producir documentos manualmente para tu pequeña o mediana empresa. Una de las mejores maneras de asegurar la calidad y utilidad de tus contratos y acuerdos es adoptar una solución multipropósito como DocHub.
La flexibilidad de edición se considera el beneficio más importante de DocHub. Utiliza herramientas robustas de uso múltiple para agregar y eliminar, o modificar cualquier elemento de un permiso. Deja comentarios, resalta información importante, establece índices en el permiso y transforma la administración de documentos en un procedimiento fácil e intuitivo. Accede a tus documentos en cualquier momento y aplica nuevas modificaciones cuando lo necesites, lo que podría reducir considerablemente tu tiempo haciendo el mismo documento desde cero.
Genera Plantillas reutilizables para simplificar tus rutinas diarias y evitar copiar y pegar la misma información continuamente. Modifícalas, agrégalas y cámbialas en cualquier momento para asegurarte de que estás en la misma página con tus socios y clientes. DocHub te ayuda a evitar errores en documentos de uso frecuente y te proporciona formularios de la más alta calidad. Asegúrate de mantener las cosas profesionales y estar en línea con tus documentos más utilizados.
Benefíciate de la modificación de permisos sin pérdida y del intercambio y almacenamiento seguro de documentos con DocHub. No pierdas más archivos ni te sientas confundido o desorientado al negociar acuerdos y contratos. DocHub empodera a los especialistas en todas partes para adoptar la transformación digital como un elemento de la gestión del cambio de su empresa.
aquí vamos a ver la noción de un conjunto de índices y las intersecciones y uniones sobre conjuntos indexados así que veamos la definición así que queremos comenzar con i donde eso es cualquier conjunto y realmente quiero decir cualquier conjunto aquí hay algunas elecciones generalmente estándar para conjuntos de índices pero realmente puedes tomarlo como arbitrario pero la única regla que necesitas es que para todo pequeño i y mayúscula i podemos producir algún conjunto a sub i y luego queríamos encontrar la unión sobre todos estos conjuntos y la intersección sobre todos estos conjuntos así que la unión sobre los ai a medida que i corre desde todo este conjunto de índices mayúscula i así que eso va a ser todo x que satisface esta regla así que x está en aj para al menos un j y i así que puedes pensar en esto como una declaración de al menos uno como si fuera una declaración o y luego la siguiente la intersección de los a i sobre este conjunto de índices es todo x que satisface esta regla así que x está en aj para todos j y i así que aquí puedes pensar en esto para todos como una declaración y si quieres relacionar th
