Establecer atributo en FDX

Cómo establecer atributos en FDX más rápido

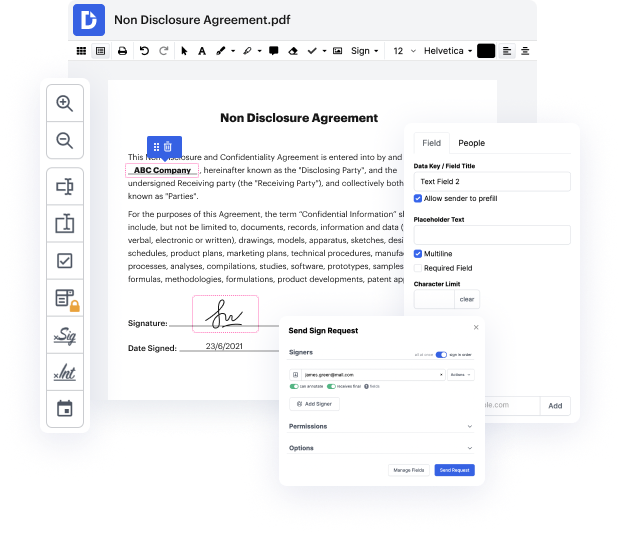
Cuando editas documentos en varios formatos a diario, la universalidad de la solución de documentos importa mucho. Si tus herramientas solo funcionan para algunos de los formatos populares, podrías encontrarte cambiando entre ventanas de aplicaciones para establecer atributos en FDX y manejar otros formatos de archivo. Si deseas quitarte el dolor de cabeza de la edición de documentos, opta por una plataforma que pueda manejar cualquier extensión sin esfuerzo.

Con DocHub, no necesitas concentrarte en nada aparte de la edición real de documentos. No necesitarás hacer malabares con aplicaciones para trabajar con diferentes formatos. Puede ayudarte a editar tu FDX tan fácilmente como cualquier otra extensión. Crea documentos FDX, edítalos y compártelos en una única plataforma de edición en línea que te ahorra tiempo y mejora tu productividad. Todo lo que tienes que hacer es registrarte en DocHub, lo cual solo toma unos minutos.

Sigue estos pasos para establecer atributos en FDX en un abrir y cerrar de ojos

Visita el sitio web de DocHub y regístrate haciendo clic en el botón Crear cuenta gratuita.
Proporciona tu correo electrónico y crea una contraseña de seguridad para registrar tu nueva cuenta o conecta tu información personal a través de tu cuenta de Gmail.
Ve al Tablero y añade el FDX que necesitas revisar. Hazlo subiendo tu archivo o enlazándolo desde la nube o donde lo tengas almacenado.
Abre el archivo en modo de edición y luego realiza todos los cambios utilizando la barra de herramientas superior.
Cuando termines de editar, utiliza el método más conveniente para guardar tu documento: descárgalo, mantenlo en tu cuenta o envíalo directamente a tu destinatario a través de DocHub.

No tendrás que convertirte en un multitarea de edición con DocHub. Su conjunto de características es suficiente para una edición rápida de documentos, independientemente del formato que desees revisar. Comienza creando una cuenta para ver lo fácil que puede ser la gestión de documentos teniendo una herramienta diseñada específicamente para tus necesidades.

Edición de PDF simplificada con DocHub

Edición de PDF sin complicaciones

Editar un PDF es tan simple como trabajar en un documento de Word. Puedes agregar texto, dibujos, resaltados y ocultar o anotar tu documento sin afectar su calidad. Sin texto rasterizado ni campos eliminados. Usa un editor de PDF en línea para obtener tu documento perfecto en minutos.

Trabajo en equipo fluido

Colabora en documentos con tu equipo usando un dispositivo de escritorio o móvil. Permite que otros vean, editen, comenten y firmen tus documentos en línea. También puedes hacer tu formulario público y compartir su URL en cualquier lugar.

Guardado automático

Cada cambio que realices en un documento se guarda automáticamente en la nube y se sincroniza en todos los dispositivos en tiempo real. No es necesario enviar nuevas versiones de un documento o preocuparse por perder información.

Integraciones de Google

DocHub se integra con Google Workspace para que puedas importar, editar y firmar tus documentos directamente desde tu Gmail, Google Drive y Dropbox. Cuando termines, exporta documentos a Google Drive o importa tu libreta de direcciones de Google y comparte el documento con tus contactos.

Potentes herramientas de PDF en tu dispositivo móvil

Mantén tu trabajo en marcha incluso cuando estés lejos de tu ordenador. DocHub funciona en móvil con la misma facilidad que en escritorio. Edita, anota y firma documentos desde la comodidad de tu teléfono inteligente o tableta. No es necesario instalar la aplicación.

Compartición y almacenamiento de documentos seguros

Comparte, envía por correo electrónico y envía documentos por fax instantáneamente de una manera segura y conforme. Establece una contraseña, coloca tus documentos en carpetas encriptadas y habilita la autenticación del destinatario para controlar quién tiene acceso a tus documentos. Una vez finalizado, mantiene tus documentos seguros en la nube.

Aumenta la eficiencia con el complemento DocHub para Google Workspace

Accede a documentos y edítalos, fírmalos y compártelos directamente desde tus aplicaciones de Google favoritas.

Instalar ahora

Cómo hacer Establecer atributo en FDX

4.8 de 5

17 votos

hola totes bienvenidos a tech TOCOM antes de que vayamos y aprendamos cómo encontrar la clave candidata queremos entender qué es el cierre de un atributo ok será útil al encontrar la clave candidata así que aprendamos qué es el cierre de un atributo primero comenzaremos con un ejemplo obviamente aquí tomemos un ejemplo simple ok y tenemos dependencias funcionales a determina B b determina D c determina B algo así bueno así que ahora si decimos qué es el cierre de un atributo significa por ejemplo el cierre del atributo a que se denota por a más así que el cierre de un atributo es el conjunto de atributos que se pueden determinar con este atributo a así que el cierre del atributo a será el conjunto de atributos que se pueden determinar con a así que si consideramos aquí en este conjunto particular de dependencias funcionales si tienes a puedes determinar B de manera única ok así que si tienes a puedes determinar de manera única quiero decir desde a siempre puedes determinar a correcto si tienes a tienes a ahora puedes determinar B ok así que si tienes B

¿Tienes preguntas?

A continuación, algunas preguntas comunes de nuestros clientes que pueden proporcionarte la respuesta que buscas. Si no puedes encontrar una respuesta a tu pregunta, no dudes en ponerte en contacto con nosotros.

Contacto

¿Cómo establecer el valor de un atributo en XML?

Los atributos XML deben estar entre comillas o así: Si el valor del atributo contiene comillas dobles, puedes usar comillas simples, como en este ejemplo: ...

¿Cómo se establecen los atributos?

setAttribute() Establece el valor de un atributo en el elemento especificado. Si el atributo ya existe, el valor se actualiza; de lo contrario, se agrega un nuevo atributo con el nombre y valor especificados. Para obtener el valor actual de un atributo, usa getAttribute(); para eliminar un atributo, llama a removeAttribute().

¿Es posible asignar atributos a una función?

Las funciones también son objetos. Por lo tanto, las funciones también deben tener atributos asignables.

¿Cómo añado ATTR?

método attr() para agregar los atributos. Aquí, estamos agregando el atributo placeholder al campo de entrada. Sintaxis: $("#add-attr").

¿Cómo usar attr en HTML?

Atributos HTML Todos los elementos HTML pueden tener atributos. Los atributos proporcionan información adicional sobre los elementos. Los atributos siempre se especifican en la etiqueta de inicio. Los atributos generalmente vienen en pares nombre/valor como: name="value"

¿Qué hace set attribute?

setAttribute() Establece el valor de un atributo en el elemento especificado. Si el atributo ya existe, el valor se actualiza; de lo contrario, se agrega un nuevo atributo con el nombre y valor especificados. Para obtener el valor actual de un atributo, usa getAttribute(); para eliminar un atributo, llama a removeAttribute().

¿Cómo establecer el valor de un atributo en CSS?

CSS [attribute^="value"] Selector El selector [attribute^="value"] se utiliza para seleccionar elementos con el atributo especificado, cuyo valor comienza con el valor especificado. El siguiente ejemplo selecciona todos los elementos con un valor de atributo de clase que comienza con "top": Nota: ¡El valor no tiene que ser una palabra completa!

¿Cómo establezco mi ATTR?

Element.setAttribute() Establece el valor de un atributo en el elemento especificado. Si el atributo ya existe, el valor se actualiza; de lo contrario, se agrega un nuevo atributo con el nombre y valor especificados. Para obtener el valor actual de un atributo, usa getAttribute(); para eliminar un atributo, llama a removeAttribute().

¿Son los atributos mejores que los valores en Roblox?

Los atributos son mucho mejores que los valores, no tienes que usar :Clone() o Instance.new() lo que hace que no uses parte de tu memoria, pero una cosa que desearía que tuvieran los atributos es un tipo de objeto, similar a ObjectValue.

¿Cómo establecer el valor de un atributo de XML en C#?

XmlElement formData = (XmlElement)xmlDoc.SelectSingleNode("//FormData"); if (formData != null) { formData.SetAttribute("FormId", "newValue"); // Establecer a nuevo valor. }

Ve por qué nuestros clientes eligen DocHub

Gran solución para documentos PDF con muy poco conocimiento previo requerido.

"Simplicidad, familiaridad con el menú y fácil de usar. Es fácil de navegar, hacer cambios y editar lo que necesites. Como se utiliza junto a Google, el documento siempre se guarda, así que no tienes que preocuparte por ello."

Pam Driscoll F
Profesora

Un valioso firmador de documentos para pequeñas empresas.

"Me encanta que DocHub sea increíblemente asequible y personalizable. Realmente hace todo lo que necesito, sin un gran precio como algunos de sus competidores más conocidos. Puedo enviar documentos seguros directamente a los correos electrónicos de mis clientes y en tiempo real cuando están viendo y haciendo alteraciones a un documento."

Jiovany A
Pequeña Empresa

Puedo crear copias rellenables para las plantillas que selecciono y luego puedo publicarlas.

"Me gusta trabajar y organizar mi trabajo de la manera adecuada para cumplir e incluso superar las demandas que se hacen a diario en la oficina, así que disfruto trabajar con archivos PDF, creo que son más profesionales y versátiles, permiten..."

Victoria G
Pequeña Empresa

esté listo para obtener más

Edita y firma PDFgratis

Empieza ahora

Búsquedas relacionadas

establecer atributo python establecer atributo jquery cambiar valor de atributo javascript estableceratributo javascript estableceratributo estilo estableceratributo no es una función estableceratributo onclick eliminar atributo javascript

Establecer atributo en FDX sin problemas