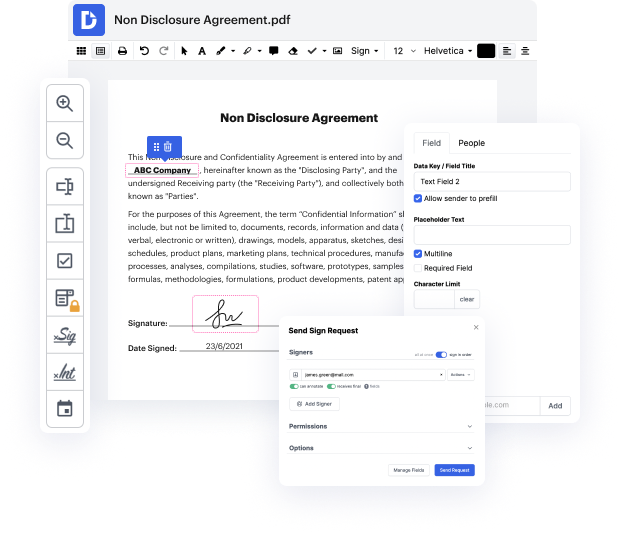
Existen numerosas soluciones de edición de documentos en el mercado, pero solo unas pocas son adecuadas para todos los formatos de archivo. Algunas herramientas son, por el contrario, versátiles pero difíciles de usar. DocHub proporciona la solución a estos inconvenientes con su editor basado en la nube. Ofrece ricas capacidades que te permiten completar tus tareas de gestión de documentos de manera eficiente. Si necesitas reemplazar rápidamente una forma en EZW, ¡DocHub es la mejor opción para ti!
Nuestro proceso es muy fácil: subes tu archivo EZW a nuestro editor → se transforma instantáneamente a un formato editable → aplicas todos los cambios requeridos y lo actualizas profesionalmente. Solo necesitas un par de momentos para completar tu trabajo de papeleo.
Una vez que se apliquen todas las modificaciones, puedes convertir tu trabajo de papeleo en una plantilla reutilizable. Simplemente necesitas ir al Menú del lado izquierdo de nuestro editor y hacer clic en Acciones → Convertir en Plantilla. Encontrarás tu trabajo de papeleo almacenado en una carpeta separada en tu Tablero, ahorrándote tiempo la próxima vez que necesites el mismo formulario. ¡Prueba DocHub hoy!
En la última clase cubrimos cómo usar la transformada de wavelet discreta en imágenes, luego también habíamos planeado cubrir cómo se codifican realmente los coeficientes de la DWT para generar el flujo de bits. Ahora no pudimos cubrir exactamente hasta el punto que habíamos decidido en la última clase debido a una falta de tiempo, así que vamos a continuar con eso en esta conferencia. El título que tenemos para esta conferencia es codificación de wavelet de árbol cero embebido. Ahora, hacia el final de la última conferencia, yo realmente les había introducido el concepto de la relación padre-hijo que existe entre los coeficientes en las diferentes subbandas y especialmente habíamos visto que cada vez que cambiamos de una resolución a la siguiente; a las resoluciones más finales cada vez que vamos, allí encontramos que un píxel o un coeficiente en la resolución más gruesa o escala más gruesa corresponde a cuatro coeficientes en el siguiente nivel final de escala y esto es lo que formará una especie de árbol donde la raíz