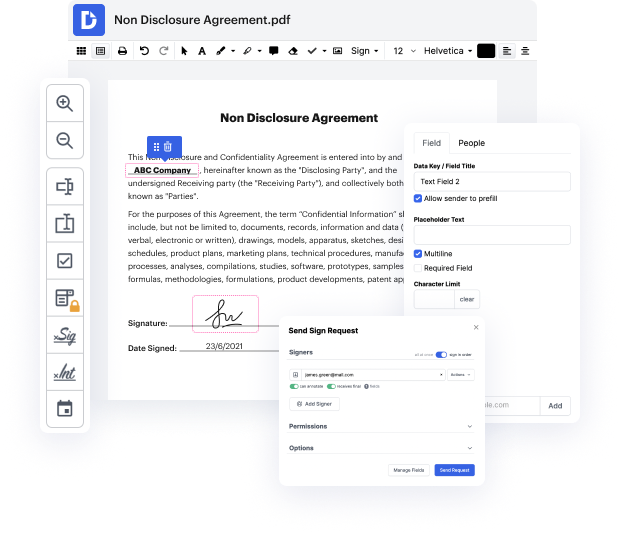
Cuando el alcance de tus tareas diarias consiste en mucha edición de documentos, ya sabes que cada formato de documento requiere su propio enfoque y, en algunos casos, software particular. Manejar un archivo binario aparentemente simple puede a menudo detener todo el proceso, especialmente si intentas editar con herramientas inadecuadas. Para evitar tales problemas, consigue un editor que pueda cubrir todas tus necesidades sin importar el formato del archivo y pegar una etiqueta en binario sin obstáculos.
Con DocHub, vas a trabajar con una herramienta de edición multifuncional para prácticamente cualquier situación o tipo de documento. Minimiza el tiempo que solías dedicar a navegar por las características de tu antiguo software y aprende de nuestra interfaz de usuario intuitiva mientras realizas el trabajo. DocHub es una plataforma de edición en línea optimizada que maneja todas tus necesidades de procesamiento de documentos para prácticamente cualquier archivo, como binario. Ábrelo y ve directamente a la eficiencia; no se requiere capacitación previa ni lectura de instrucciones para aprovechar los beneficios que DocHub aporta a la gestión de documentos. Comienza dedicando un par de minutos a registrar tu cuenta ahora.
Observa mejoras en el procesamiento de tus documentos justo después de abrir tu perfil de DocHub. Ahorra tiempo en la edición con nuestra única solución que puede ayudarte a ser más productivo con cualquier formato de archivo con el que tengas que trabajar.
este video va a analizar la relación entre el número de bits y el número de patrones que son posibles para el número de bits dado que el elemento de almacenamiento más simple a menudo se refiere como un flip-flop es útil pensar en un flip-flop como un diagrama esquemático como se muestra aquí simplemente una caja o un área en la que puedes almacenar un bit así que cuando consideramos un flip-flop podemos decir que un flip-flop puede almacenar un bit y este bit puede ser un cero o puede ser un uno consideremos un patrón de bits los bits pueden agruparse para producir muchos patrones diferentes consideremos un flip-flop y añadamos a él otro flip-flop y ahora podemos considerar qué bits se pueden colocar en cada uno de los flip-flops y cuántos patrones se pueden producir bueno consideremos que ambos flip-flops pueden almacenar un cero como puedes ver otra combinación que podemos tener se muestra aquí otra y finalmente la última combinación posible cuando tienes dos bits consideremos ahora tres flip-flops unidos y cuántas dif