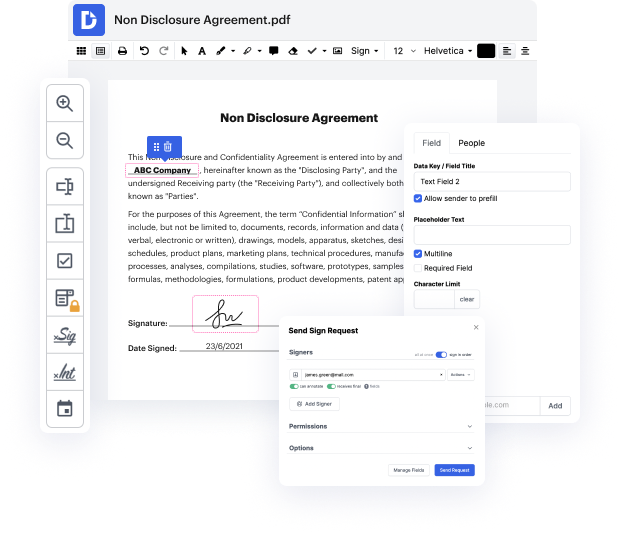
Ya sea que estés acostumbrado a trabajar con binarios o que estés gestionando este formato por primera vez, editarlo no debería parecer un desafío. Diferentes formatos pueden requerir software específico para abrirlos y editarlos correctamente. Sin embargo, si necesitas vincular rápidamente leyendas en binario como parte de tu proceso habitual, lo mejor es encontrar una herramienta multifuncional de documentos que permita todo tipo de operaciones sin esfuerzo adicional.
Prueba DocHub para una edición elegante de binarios y también otros formatos de documentos. Nuestra plataforma proporciona un procesamiento de documentos sencillo, sin importar cuánta o poca experiencia previa tengas. Con las herramientas que necesitas para trabajar en cualquier formato, no tendrás que cambiar entre ventanas de edición al trabajar con cada uno de tus documentos. Crea, edita, anota y comparte tus documentos sin esfuerzo para ahorrar tiempo en tareas menores de edición. Solo necesitarás registrar una nueva cuenta de DocHub, y luego podrás comenzar tu trabajo de inmediato.
Observa una mejora en la productividad del procesamiento de documentos con el conjunto de características simples de DocHub. Edita cualquier documento de manera fácil y rápida, independientemente de su formato. Disfruta de todos los beneficios que provienen de la eficiencia y conveniencia de nuestra plataforma.
Hola, ¿qué tal chicos? Anuj aquí, bienvenidos al curso de DSA One. En el video de hoy resolveremos la pregunta que es convertir un árbol binario en una lista doblemente enlazada. Es una pregunta de entrevista muy famosa, es una pregunta genérica que se pregunta comúnmente y la forma de resolverla, la forma optimizada, entenderemos el código de eso, mejorará tu conocimiento sobre la recursión. La pregunta es muy fácil, te dan un árbol binario y tienes que convertirlo en una lista doblemente enlazada. Dirás que es muy fácil, podemos convertirlo fácilmente. Déjame decirte cómo tienes que convertirlo. Hay una restricción que es que la salida debe estar en el recorrido en orden del árbol binario. Así que si este es tu árbol binario, la lista doblemente enlazada para esto estará en forma ordenada de este árbol. Supongamos que este es tu árbol binario, entonces el recorrido en orden para esto será este. Hemos visto el recorrido en orden, hemos visto el recorrido en orden, preorden y postorden también. Si no sabes sobre eso, puedes ver ese video y entonces podrás entender esto.