Inicio
Funcionalidad
Utiliza nuestras funciones de edición de documentos PDF directamente en tu navegador sin complicaciones
Grupo de Características de Papel Gratis

Descubre la forma más rápida de Grupo Característica Papel Gratis

Aug 6th, 2022

formularios completados

formularios firmados

formularios enviados

01. Carga un documento desde tu ordenador o almacenamiento en la nube.

02. Agrega texto, imágenes, dibujos, formas, y más.

03. Firma tu documento en línea en unos pocos clics.

04. Envía, exporta, envía por fax, descarga o imprime tu documento.

La forma más rápida de Grupo Característica Papel Gratis con DocHub

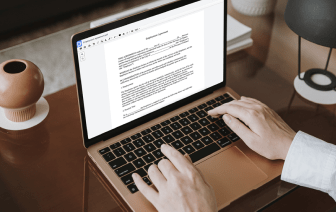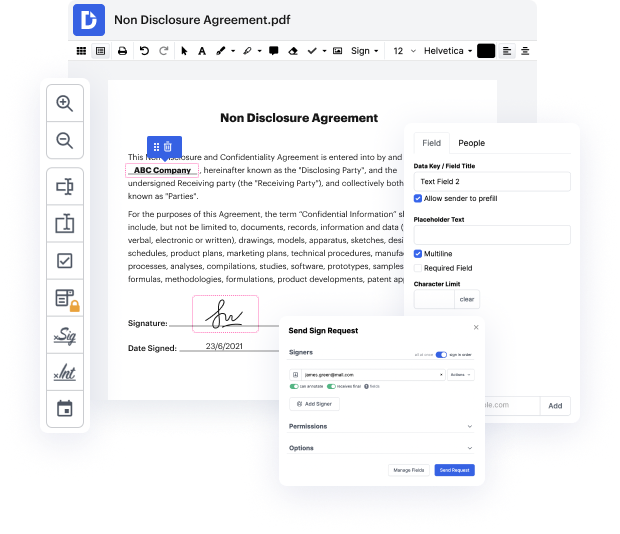
¿Estás buscando un editor que te permita hacer esa edición de última hora y Grupo Característica Papel Gratis? ¡Entonces estás en el camino correcto! Con DocHub, puedes aplicar rápidamente cualquier cambio necesario a tu documento, sin importar su formato de archivo. Tus archivos de salida se verán más profesionales y estructurados; no es necesario descargar ningún software que ocupe mucho espacio. Puedes usar nuestro editor desde la comodidad de tu navegador.

Selecciona cualquier método disponible para agregar un documento, trae uno de la nube, arrastra y suelta tu archivo, o agrégalo a través de un enlace, etc.
Una vez cargado, DocHub se abrirá con un editor fácil de usar y directo.
Descubre la barra de herramientas superior, para localizar una variedad de funciones que te permiten anotar, editar y completar, y trabajar con documentos como un usuario avanzado.
Localiza la opción para Grupo Característica Papel Gratis y aplícala a tu documento. Haz clic en el botón deshacer para descartar esta acción.
Si estás satisfecho con la versión final de tu documento, elige qué te gustaría hacer con el archivo seleccionando la opción necesaria de la barra de herramientas superior.
Comparte tu archivo directamente desde DocHub con tu equipo, descárgalo, o simplemente guárdalo para continuar trabajando en él más tarde.

Al usar nuestro editor, mantente tranquilo sabiendo que tu información sensible está protegida y alejada de miradas curiosas. Cumplimos con importantes regulaciones de protección de datos y comercio electrónico para garantizar que tu experiencia sea libre de riesgos y placentera en cada punto de interacción con nuestro editor. Si necesitas ayuda para optimizar tu documento, nuestro equipo de soporte dedicado siempre está listo para responder todas tus consultas. También puedes aprovechar nuestro avanzado centro de conocimiento para autoayuda.

¡Prueba nuestro editor hoy y Grupo Característica Papel Gratis con facilidad!

Edición de PDF simplificada con DocHub

Edición de PDF sin complicaciones

Editar un PDF es tan simple como trabajar en un documento de Word. Puedes agregar texto, dibujos, resaltados y ocultar o anotar tu documento sin afectar su calidad. Sin texto rasterizado ni campos eliminados. Usa un editor de PDF en línea para obtener tu documento perfecto en minutos.

Trabajo en equipo fluido

Colabora en documentos con tu equipo usando un dispositivo de escritorio o móvil. Permite que otros vean, editen, comenten y firmen tus documentos en línea. También puedes hacer tu formulario público y compartir su URL en cualquier lugar.

Guardado automático

Cada cambio que realices en un documento se guarda automáticamente en la nube y se sincroniza en todos los dispositivos en tiempo real. No es necesario enviar nuevas versiones de un documento o preocuparse por perder información.

Integraciones de Google

DocHub se integra con Google Workspace para que puedas importar, editar y firmar tus documentos directamente desde tu Gmail, Google Drive y Dropbox. Cuando termines, exporta documentos a Google Drive o importa tu libreta de direcciones de Google y comparte el documento con tus contactos.

Potentes herramientas de PDF en tu dispositivo móvil

Mantén tu trabajo en marcha incluso cuando estés lejos de tu ordenador. DocHub funciona en móvil con la misma facilidad que en escritorio. Edita, anota y firma documentos desde la comodidad de tu teléfono inteligente o tableta. No es necesario instalar la aplicación.

Compartición y almacenamiento de documentos seguros

Comparte, envía por correo electrónico y envía documentos por fax instantáneamente de una manera segura y conforme. Establece una contraseña, coloca tus documentos en carpetas encriptadas y habilita la autenticación del destinatario para controlar quién tiene acceso a tus documentos. Una vez finalizado, mantiene tus documentos seguros en la nube.

Aumenta la eficiencia con el complemento DocHub para Google Workspace

Accede a documentos y edítalos, fírmalos y compártelos directamente desde tus aplicaciones de Google favoritas.

Instalar ahora

Cómo hacer Grupo de Características de Papel Gratis

4.8 de 5

25 votos

hola, así que hoy quiero hablar sobre tonterías abstractas um un ejemplo de tonterías abstractas ahora las tonterías abstractas se refieren a teoremas y pruebas que están relacionadas con la teoría de categorías la teoría de categorías involucra objetos y flechas y diagramas conmutativos como el que he dibujado aquí ahora quiero hablar más específicamente sobre un tema en teoría de grupos conocido como la noción de un grupo libre ok un grupo libre sobre un conjunto X ahora, ¿qué es realmente lo que estamos tratando de lograr con esta definición? estamos tratando de construir un grupo que en un sentido coloquial tiene los elementos de X como su conjunto de generadores y no satisface ninguna relación innecesaria, sabes, no hay ecuaciones algebraicas innecesarias que se sostengan en este grupo además de las que son forzadas por el hecho de que es un grupo ok así que um para motivar esto pensamos en ok um tenemos cosas como grupos simétricos grupos diédricos podemos definir estas cosas um de muchas maneras podemos decir ok el grupo simétrico es el

Funciones relacionadas

Include sentence in the Travel Information

Include sentence in the Free Admission Ticket

Include sentence in the Exit Ticket

Include sentence in the Reservation Template for Gala

Include sentence in the Live Performance Event Ticket

Include sentence in the Carnival Ticket

Include sentence in the Fundraiser Ticket

Include sentence in the Children's Concert Ticket

Ve por qué nuestros clientes eligen DocHub

Gran solución para documentos PDF con muy poco conocimiento previo requerido.

"Simplicidad, familiaridad con el menú y fácil de usar. Es fácil de navegar, hacer cambios y editar lo que necesites. Como se utiliza junto a Google, el documento siempre se guarda, así que no tienes que preocuparte por ello."

Pam Driscoll F
Profesora

Un valioso firmador de documentos para pequeñas empresas.

"Me encanta que DocHub sea increíblemente asequible y personalizable. Realmente hace todo lo que necesito, sin un gran precio como algunos de sus competidores más conocidos. Puedo enviar documentos seguros directamente a los correos electrónicos de mis clientes y en tiempo real cuando están viendo y haciendo alteraciones a un documento."

Jiovany A
Pequeña Empresa

Puedo crear copias rellenables para las plantillas que selecciono y luego puedo publicarlas.

"Me gusta trabajar y organizar mi trabajo de la manera adecuada para cumplir e incluso superar las demandas que se hacen a diario en la oficina, así que disfruto trabajar con archivos PDF, creo que son más profesionales y versátiles, permiten..."

Victoria G
Pequeña Empresa

esté listo para obtener más

Edita y firma PDFgratis

Empieza ahora

Búsquedas relacionadas

papel de características mdpi invitación de papel de características descarga de papeles software de papeles descarga de papeles readcube papeles readcube papeles 3 aplicación de papeles