Incrustar espacio en CCF - Herramienta de edición en línea

Tu herramienta de confianza para incrustar espacio en CCF, sin descargas requeridas

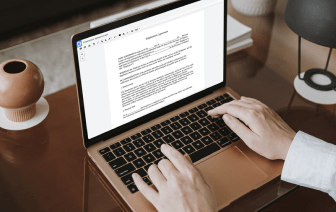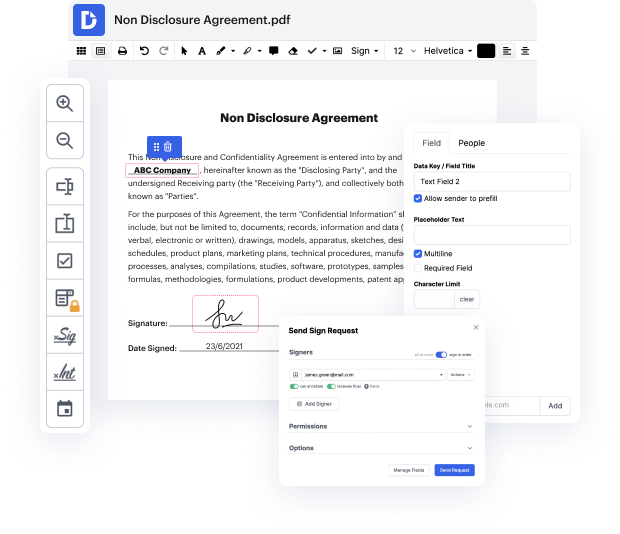
No todos los formatos, incluido CCF, están desarrollados para ser fácilmente editables. A pesar de que muchas capacidades pueden ayudarnos a modificar todos los formatos de archivo, nadie ha inventado aún una solución real que sirva para todos.

DocHub ofrece una solución sencilla y optimizada para editar, gestionar y almacenar documentos en los formatos más utilizados. No tienes que ser una persona con conocimientos tecnológicos para incrustar espacio en CCF o hacer otros ajustes. DocHub es lo suficientemente robusto como para hacer que el proceso sea sencillo para todos.

Nuestra herramienta te permite alterar y ajustar documentos, enviar datos de un lado a otro, crear formularios dinámicos para la recolección de información, cifrar y proteger documentos, y configurar flujos de trabajo de firma electrónica. Además, también puedes generar plantillas a partir de documentos que utilizas regularmente.

Encontrarás muchas herramientas adicionales dentro de DocHub, incluidas integraciones que te permiten vincular tu archivo CCF a una variedad de aplicaciones de productividad.

Cómo incrustar espacio en CCF

Navega a la página principal de DocHub y haz clic en Iniciar sesión.
Importa tu archivo al editor utilizando una de las numerosas opciones de importación.
Utiliza diferentes capacidades para aprovechar al máximo nuestro editor. En la barra de menú, selecciona la capacidad de incrustar espacio en CCF.
Verifica el texto en tu documento en busca de errores y faltas de ortografía y asegúrate de que se vea optimizado para la web.
Después de finalizar el proceso de edición, haz clic en HECHO.
Selecciona qué necesitas hacer con el documento a continuación: reorganizarlo, compartirlo como un enlace, enviarlo por fax, etc.

DocHub es una forma sencilla y a un precio razonable de gestionar documentos y simplificar flujos de trabajo. Ofrece una amplia gama de capacidades, desde la creación hasta la edición, servicios profesionales de firma electrónica y creación de documentos web. El programa puede exportar tus documentos en muchos formatos mientras mantiene la máxima seguridad y sigue los más altos estándares de seguridad de la información.

Pruébalo y descubre lo sencillo que puede ser tu proceso de edición.

Edición de PDF simplificada con DocHub

Edición de PDF sin complicaciones

Editar un PDF es tan simple como trabajar en un documento de Word. Puedes agregar texto, dibujos, resaltados y ocultar o anotar tu documento sin afectar su calidad. Sin texto rasterizado ni campos eliminados. Usa un editor de PDF en línea para obtener tu documento perfecto en minutos.

Trabajo en equipo fluido

Colabora en documentos con tu equipo usando un dispositivo de escritorio o móvil. Permite que otros vean, editen, comenten y firmen tus documentos en línea. También puedes hacer tu formulario público y compartir su URL en cualquier lugar.

Guardado automático

Cada cambio que realices en un documento se guarda automáticamente en la nube y se sincroniza en todos los dispositivos en tiempo real. No es necesario enviar nuevas versiones de un documento o preocuparse por perder información.

Integraciones de Google

DocHub se integra con Google Workspace para que puedas importar, editar y firmar tus documentos directamente desde tu Gmail, Google Drive y Dropbox. Cuando termines, exporta documentos a Google Drive o importa tu libreta de direcciones de Google y comparte el documento con tus contactos.

Potentes herramientas de PDF en tu dispositivo móvil

Mantén tu trabajo en marcha incluso cuando estés lejos de tu ordenador. DocHub funciona en móvil con la misma facilidad que en escritorio. Edita, anota y firma documentos desde la comodidad de tu teléfono inteligente o tableta. No es necesario instalar la aplicación.

Compartición y almacenamiento de documentos seguros

Comparte, envía por correo electrónico y envía documentos por fax instantáneamente de una manera segura y conforme. Establece una contraseña, coloca tus documentos en carpetas encriptadas y habilita la autenticación del destinatario para controlar quién tiene acceso a tus documentos. Una vez finalizado, mantiene tus documentos seguros en la nube.

Aumenta la eficiencia con el complemento DocHub para Google Workspace

Accede a documentos y edítalos, fírmalos y compártelos directamente desde tus aplicaciones de Google favoritas.

Instalar ahora

Cómo hacer incrustar espacio en CCF

4.8 de 5

41 votos

uh también hablamos sobre otra representación importante de forma canónica que es la forma canónica diagonal uh para demostrar este procedimiento comenzamos nuevamente con la misma función de transferencia y reescribimos esta función de transferencia uh en otros formatos ahora para obtener la representación de forma canónica diagonal básicamente hemos factorizado este polinomio así que es s más 2 S más 3 S más 4 hemos factorizado este polinomio del denominador aquí y a continuación obtenemos la expansión en fracciones parciales que se da aquí así que esta función de transferencia es igual a esta expresión ya conoces el procedimiento para obtener esta expansión en fracciones parciales uh puedes verificar sumando todos estos términos que finalmente obtienes nuevamente la misma función de transferencia así que esta función de transferencia se reescribe en este formato particular que es teníamos esta función de transferencia la hemos reescrito en este formato particular uh U de S multiplicado por esta función de transferencia y U de S multiplicado por esta función de transferencia U de S multip

Funciones relacionadas

Eliminar el campo de moneda de la UE en la demanda

Eliminar la configuración de campo en la demanda

Eliminar configuraciones de campo de la demanda

Eliminar la configuración de campo a la demanda

Eliminar configuraciones de campo en la demanda

Eliminar la validación de campo en la demanda

Eliminar la validación de campo de la demanda

Eliminar la validación de campo a la demanda

¿Tienes preguntas?

A continuación, algunas preguntas comunes de nuestros clientes que pueden proporcionarte la respuesta que buscas. Si no puedes encontrar una respuesta a tu pregunta, no dudes en ponerte en contacto con nosotros.

Contacto

¿Cómo importo un conjunto de datos de Hugging Face?

Hugging Face Hub Comienza creando un repositorio de datos y sube tus archivos de datos. Ahora puedes usar la función loaddataset() para cargar el conjunto de datos. dataset = loaddataset( lhoestq/customsquad, revision=main # nombre de la etiqueta, o nombre de la rama, o hash de confirmación )

¿Qué es un espacio en Hugging Face?

Hugging Face Spaces ofrece una forma sencilla de alojar aplicaciones de demostración de ML directamente en tu perfil o en el perfil de tu organización. Esto te permite crear tu portafolio de ML, mostrar tus proyectos en conferencias o a partes interesadas, y trabajar de manera colaborativa con otras personas en el ecosistema de ML.

¿Cómo crear un espacio en Hugging Face?

Para hacer un nuevo Espacio, visita la página principal de Spaces y haz clic en Crear nuevo Espacio. Junto con elegir un nombre para tu Espacio, seleccionar una licencia opcional y establecer la visibilidad de tu Espacio, se te pedirá que elijas el SDK para tu Espacio.

¿Cómo hacer un push a un espacio de Hugging Face?

Empujar el repositorio de Github al espacio de Huggingface Colócalo en los secretos del repositorio con un nombre como HF en la configuración del repositorio de Github relacionado: . está en la forma de: models: /

¿Cómo incrustar un espacio en una URL?

Las URL no pueden contener espacios. La codificación de URL normalmente reemplaza un espacio con un signo más (+) o con %20.

¿Cómo incrustar un espacio de huggingface?

URL directa Un Espacio se asigna a una URL única que puedes usar para compartir tu Espacio o incrustarlo en un sitio web. Esta URL es de la forma: . Por ejemplo, el Espacio NimaBoscarino/hotdog-gradio tiene la URL correspondiente de .

¿Cómo ejecutar espacios de Hugging Face localmente?

Intentando ejecutar un espacio localmente git lfs . git clone Enhance This HiDiffusion SDXL - un Espacio de Hugging Face por radames. python -m venv . env. envScriptsactivate. pip -r requirements. txt. pip mediapipe. pip streamlit. streamlit run app.py.

Ve por qué nuestros clientes eligen DocHub

Gran solución para documentos PDF con muy poco conocimiento previo requerido.

"Simplicidad, familiaridad con el menú y fácil de usar. Es fácil de navegar, hacer cambios y editar lo que necesites. Como se utiliza junto a Google, el documento siempre se guarda, así que no tienes que preocuparte por ello."

Pam Driscoll F
Profesora

Un valioso firmador de documentos para pequeñas empresas.

"Me encanta que DocHub sea increíblemente asequible y personalizable. Realmente hace todo lo que necesito, sin un gran precio como algunos de sus competidores más conocidos. Puedo enviar documentos seguros directamente a los correos electrónicos de mis clientes y en tiempo real cuando están viendo y haciendo alteraciones a un documento."

Jiovany A
Pequeña Empresa

Puedo crear copias rellenables para las plantillas que selecciono y luego puedo publicarlas.

"Me gusta trabajar y organizar mi trabajo de la manera adecuada para cumplir e incluso superar las demandas que se hacen a diario en la oficina, así que disfruto trabajar con archivos PDF, creo que son más profesionales y versátiles, permiten..."

Victoria G
Pequeña Empresa

esté listo para obtener más

Edita y firma PDFgratis

Empieza ahora