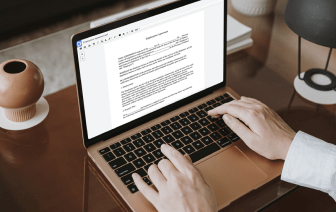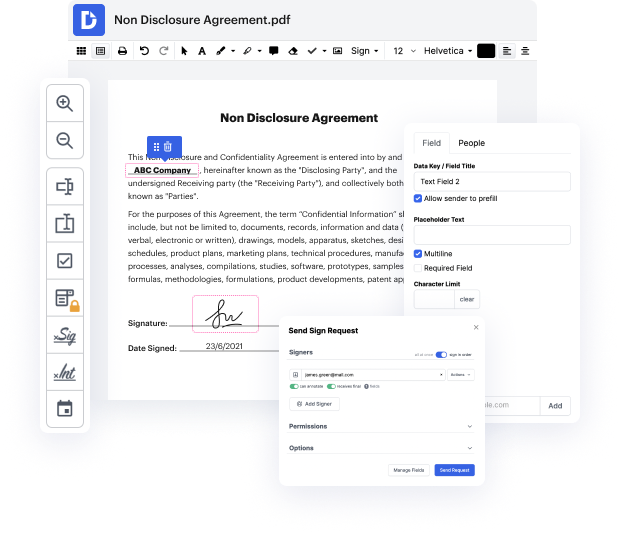
Cuando tu trabajo diario incluye mucha edición de documentos, te das cuenta de que cada formato de archivo requiere su propio enfoque y, a menudo, software particular. Manejar un archivo EZW que parece simple puede detener todo el proceso, especialmente cuando intentas editar con herramientas insuficientes. Para prevenir este tipo de dificultades, encuentra un editor que cubra todos tus requisitos sin importar la extensión del archivo y resaltar en EZW sin obstáculos.
Con DocHub, trabajarás con una herramienta de edición multifuncional para prácticamente cualquier situación o tipo de archivo. Minimiza el tiempo que solías dedicar a navegar por las características de tu antiguo software y aprende de nuestra interfaz intuitiva mientras realizas el trabajo. DocHub es una plataforma de edición en línea optimizada que cubre todos tus requisitos de procesamiento de archivos para cualquier archivo, incluyendo EZW. Ábrelo y ve directamente a la productividad; no se requiere capacitación previa ni leer guías para disfrutar de los beneficios que DocHub aporta a la gestión de documentos. Comienza dedicando unos minutos a crear tu cuenta ahora.
Ve las mejoras en el procesamiento de tu documento inmediatamente después de abrir tu cuenta de DocHub. Ahorra tiempo en la edición con nuestra solución única que te ayudará a ser más productivo con cualquier formato de documento con el que necesites trabajar.
En la última clase cubrimos cómo usar la transformada de wavelet discreta en imágenes, luego también habíamos planeado cubrir cómo se codifican realmente los coeficientes de la DWT para generar el flujo de bits. Ahora no pudimos cubrir exactamente hasta el punto que habíamos decidido en la última clase debido a una falta de tiempo, así que vamos a continuar con eso en esta conferencia. El título que tenemos para esta conferencia es codificación de wavelet de árbol cero incrustado. Ahora, hacia el final de la última conferencia, yo te había presentado el concepto de la relación padre-hijo que existe entre los coeficientes en las diferentes subbandas y especialmente habíamos visto que cada vez que cambiamos de una resolución a la siguiente; a las resoluciones más finales cada vez que vamos, allí encontramos que un píxel o un coeficiente en la resolución más gruesa o escala más gruesa corresponde a cuatro coeficientes en el siguiente nivel final de escala y esto es lo que formará una especie de árbol donde la raíz