La edición de documentos es un elemento de numerosas profesiones y carreras, que es la razón por la cual los instrumentos para ello deben estar disponibles y ser claros en cuanto a su uso. Un editor en línea avanzado puede ahorrarte muchos dolores de cabeza y ahorrar una cantidad considerable de tiempo si necesitas Integra la transcripción de línea.
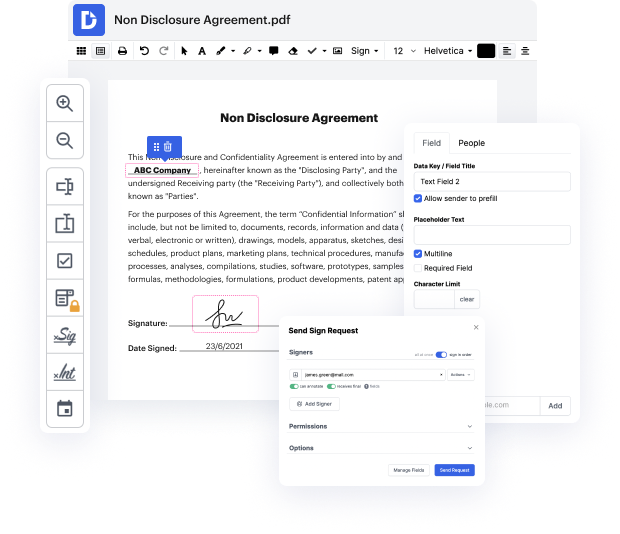
DocHub es una excelente ilustración de una herramienta que puedes dominar muy rápidamente con todas las funciones importantes a mano. Puedes comenzar a modificar instantáneamente después de crear una cuenta. La interfaz fácil de usar del editor te permitirá descubrir y utilizar cualquier función en poco tiempo. Experimenta la diferencia con el editor de DocHub tan pronto como lo abras para Integra la transcripción de línea.
Siendo una parte importante de los flujos de trabajo, la edición de documentos debe permanecer sencilla. Utilizando DocHub, puedes encontrar rápidamente tu camino alrededor del editor y hacer los ajustes necesarios a tu documento sin perder un minuto.
El profesor Dave aquí, quiero hablarte sobre integrales de línea. A estas alturas ya estamos muy familiarizados con las integrales ordinarias. Integrar f(x)dx nos permite encontrar el área bajo a una curva dada por la función f(x). Integrar f(x,y)dxdy nos permite encontrar el volumen bajo una superficie dada por la función f(x,y). Ahora, con las integrales de línea, podemos integrar a una superficie f(x,y) a lo largo del camino de alguna curva C. Estaremos integrando a lo largo de pequeños segmentos de la curva C, que llamaremos ds. Al igual que cuando aprendimos inicialmente la integración, estos segmentos serán nuestros anchos, mientras que la superficie f(x,y) será nuestra altura. Así que una vez más, nuestra integración dará un área, pero ahora estamos encontrando el área bajo una superficie a lo largo de un camino particular dentro de esa superficie. La forma en que escribiremos esto es la integración a lo largo de C de f(x,y)ds. Recuerda que cuando aprendimos a evaluar integrales múltiples, las variables x e y se trataban de manera independiente durante la integración. Pero ahora, con las integrales de línea, tenemos una única integral